题目内容
15.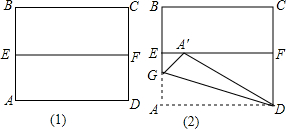 如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.
如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.
分析 由翻折变换的性质得出得出DA=DA′,在Rt△A′FD中,sin∠DA′F=$\frac{DF}{D{A}^{′}}$=$\frac{1}{2}$,得出∠DA′F=30°即可.
解答 解:由翻折变换的性质得:∠EFD=90°,DF=$\frac{1}{2}$CD,
∵四边形ABCD是正方形,
∴CD=AD,
∴DF=$\frac{1}{2}$AD,
∵DA′=AD,
∴DF=$\frac{1}{2}$DA′
∴在Rt△A′FD中,sin∠DA′F=$\frac{DF}{D{A}^{′}}$=$\frac{1}{2}$,
∴∠DA′F=30°.
点评 本题考查了翻折变换和正方形的性质、锐角三角函数;熟练掌握翻折变换的性质和正方形的性质,由三角函数求出∠DA′F是解决问题的关键.

练习册系列答案
相关题目
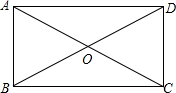 如图,矩形ABCD中,AC、BD交于点O,请你添加一个条件,使矩形ABCD成为正方形,你添加的条件是AB=BC(答案不唯一,如AC⊥BD等).
如图,矩形ABCD中,AC、BD交于点O,请你添加一个条件,使矩形ABCD成为正方形,你添加的条件是AB=BC(答案不唯一,如AC⊥BD等).
 已知,如图,在△ABC中,AB=BC,∠B=70°,则∠A=55°.
已知,如图,在△ABC中,AB=BC,∠B=70°,则∠A=55°.