题目内容
5.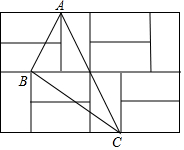 如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1,E2…表示)
(3)求sin∠ACB的值.
分析 (1)设每个小矩形的长为x,宽为y,根据图形可知小矩形的长与宽间的数量关系有两个:2个矩形的宽=矩形的长;两个矩形的宽+1个矩形的长=4,据此列出方程组,并解答即可;
(2)利用图形和勾股定理逆定理进行解答;
(3)利用面积法求得边AC上的高,然后由锐角三角函数的定义进行解答.
解答 解:(1)设每个小矩形的长为x,宽为y,
依题意得:$\left\{\begin{array}{l}{x+2y=4}\\{2y=x}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
所以每个小矩形的长为2,宽为1;
(2)如图所示: ;
;
(3)由图可知,S△ABC=4,设AC边上的高线为h,可知,$\frac{1}{2}$AC•h=4.
∵由图可计算AC=2$\sqrt{5}$,BC=$\sqrt{13}$,
∴h=$\frac{4\sqrt{5}}{5}$,
∴sin∠ACB=$\frac{h}{BC}$=$\frac{\frac{4\sqrt{5}}{5}}{\sqrt{13}}$=$\frac{4\sqrt{65}}{65}$.
点评 本题考查了四边形综合题,需要掌握二元一次方程组的应用、勾股定理、勾股定理的逆定理以及锐角三角函数的定义的应用,主要考查学生的理解能力和观察图形的能力,求三角函数值需构建直角三角形是解此类题的常用作法.

练习册系列答案
相关题目
20.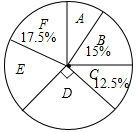 某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
根据图标提供的信息,下列结论错误的是( )
 某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)| 选修课 | A | B | C | D | E | F |
| 人数 | 20 | 30 |
| A. | 这次被调查的学生人数为200人 | |
| B. | 扇形统计图中E部分扇形的圆心角为72° | |
| C. | 被调查的学生中最想选F的人数为35人 | |
| D. | 被调查的学生中最想选D的有55人 |
10.二次函数y=-(x-2)2-3的图象的顶点坐标是( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
14. 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )| A. | 24 | B. | 30 | C. | 18 | D. | 14.4 |
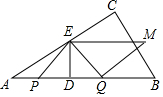 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=30,动点P、Q分别从点A、B同时出发,点P以10m/s的速度沿A→B向终点B运动,点Q以20m/s的速度沿B→A向终点A运动,过PQ的中点D作DE⊥AB交AC于点E,将△PQE绕着ED的中点旋转180°得到△MEQ,设四边形PQME的面积为S(cm2),点P运动的时间为t(s)
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=30,动点P、Q分别从点A、B同时出发,点P以10m/s的速度沿A→B向终点B运动,点Q以20m/s的速度沿B→A向终点A运动,过PQ的中点D作DE⊥AB交AC于点E,将△PQE绕着ED的中点旋转180°得到△MEQ,设四边形PQME的面积为S(cm2),点P运动的时间为t(s) 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.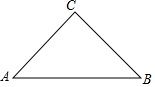 如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,将△ABC翻折,使得点B与边AC的中点M重合,如果折痕与边AB的交点为E,那么BE的长为$\frac{5\sqrt{2}}{3}$.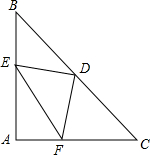 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.