题目内容
15.在直角三角形中,自两锐角顶点所引的两条中线长的平方分别为25和40,则斜边长的平方为2$\sqrt{13}$.分析 根据已知设AC=x,BC=y,在Rt△ACD和Rt△BCE中,根据勾股定理分别列等式,从而求得AC,BC的长,最后根据勾股定理即可求得AB的长.
解答  解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,
解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,
∴AD=$\sqrt{40}$=2$\sqrt{10}$,BE=$\sqrt{25}$=5,
设AC=x,BC=y
根据勾股定理得:
在Rt△ACD中,x2+($\frac{1}{2}$y)2=(2$\sqrt{10}$)2
在Rt△BCE中,($\frac{1}{2}$x)2+y2=52
解得:x=6,y=4
在Rt△ABC中,AB=$\sqrt{{6}^{2}+{4}^{2}}$=2$\sqrt{13}$,
故答案为:2$\sqrt{13}$.
点评 本题主要考查了中线的定义、勾股定理;熟练掌握勾股定理,求出AC和BC是解决问题的关键.

练习册系列答案
相关题目
14. 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )| A. | 24 | B. | 30 | C. | 18 | D. | 14.4 |
3.一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )


| A. | 2018 | B. | 2017 | C. | 2016 | D. | 2015 |
10.若将代数式4(x+8)写成了4x+8,则结果比原来( )
| A. | 少24 | B. | 多24 | C. | 少4 | D. | 多4 |
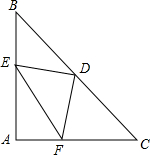 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF. 如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.
如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.