题目内容
16.(1)9$\sqrt{3}$+7$\sqrt{12}$-5$\sqrt{48}$+2$\sqrt{\frac{1}{3}}$(2)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(3)(2$\sqrt{3}$-1)(2$\sqrt{3}$+1)-(1-2$\sqrt{3}$)2.
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)先利用二次根式的乘除法则运算,然后化简后合并即可;
(3)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=9$\sqrt{3}$+14$\sqrt{3}$-20$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$=$\frac{11\sqrt{3}}{3}$;
(2)原式=$\sqrt{\frac{48}{3}}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$=4-$\sqrt{6}$+2$\sqrt{6}$=4+$\sqrt{6}$;
(3)原式=12-1-1+4$\sqrt{3}$-12=$\sqrt{3}$-2.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
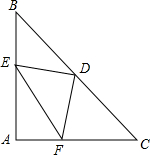 如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF.
如图,在△ABC中,AB=AC,∠A=90°,点D是BC边的中点,点E,F分别在AB,AC上.且DE⊥DF. 如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.
如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由. 如图所示是用相同的正方形砖铺成的地板,一宝物藏在某一块下面,宝物在白色区域的概率是$\frac{5}{9}$.
如图所示是用相同的正方形砖铺成的地板,一宝物藏在某一块下面,宝物在白色区域的概率是$\frac{5}{9}$.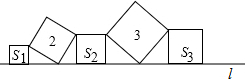
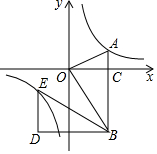 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.