题目内容
 如图,菱形ABCD的边长为5,过点A作对角线AC的垂线,交CB的延长线于点E,AE=4.
如图,菱形ABCD的边长为5,过点A作对角线AC的垂线,交CB的延长线于点E,AE=4.(1)求证:BE=BC;
(2)求S菱形ABCD.
考点:菱形的性质
专题:
分析:(1)由条件可证得∠E+∠ACB=∠EAB+∠BAC,可证得∠E=∠EAB,可得结论;
(2)由(1)的结论,结合菱形的性质可得S菱形ABCD=S△EAC,结合条件可求得答案.
(2)由(1)的结论,结合菱形的性质可得S菱形ABCD=S△EAC,结合条件可求得答案.
解答:(1)证明:∵四边形ABCD为菱形,
∴AB=BC,
∴∠BAC=∠ACB,
∵EA⊥AC,
∴∠E+∠ACB=∠EAB+∠BAC,
∴∠E=∠EAB,
∴BA=BE,
∴BE=BC;
(2)解:∵四边形ABCD为菱形,
∴△ABC≌△ADC,
∴S菱形ABCD=2S△ABC=S△EAC=
AE•AC=
×4×5=10.
∴AB=BC,
∴∠BAC=∠ACB,
∵EA⊥AC,
∴∠E+∠ACB=∠EAB+∠BAC,
∴∠E=∠EAB,
∴BA=BE,
∴BE=BC;
(2)解:∵四边形ABCD为菱形,
∴△ABC≌△ADC,
∴S菱形ABCD=2S△ABC=S△EAC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查菱形的性质,掌握菱形的四条边都相等是解题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、单项式与多项式统称为整式 |
| B、相等的角是对顶角 |
| C、两个负数比较大小绝对值大的反而小 |
| D、同角的补角相等 |
若∠1和∠2互余,∠1与∠3互补,则∠2与∠3的关系是( )
| A、∠3=90°+∠2 |
| B、∠3=90°-∠2 |
| C、∠3=180°+∠2 |
| D、∠3=180°-∠2 |
下列方程中,解为x=-1的是( )
| A、2x+3=3x-2 | ||||
| B、3(2-x)=-x+4 | ||||
| C、3(1-5x)=42 | ||||
D、
|
 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是
如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是 已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.
已知抛物线y=x2-2x+3经过点B(3,6),与y轴交于点A(0,3),若点M是直线AB:y=x+3下方抛物线上的一点,且S△ABM=3,求点M的坐标.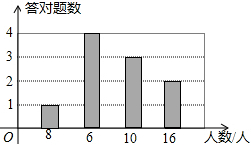 电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.
电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示. 2014年5月31日是世界卫生组织发起的第27个“世界无烟日”.为了更好地宣传吸烟的危害,某中学九年级(1)班数学兴趣小组设计了如下调查问卷,在东方广场随机调查了部分吸烟人群,并将调查结果绘制成如图所示的统计图.
2014年5月31日是世界卫生组织发起的第27个“世界无烟日”.为了更好地宣传吸烟的危害,某中学九年级(1)班数学兴趣小组设计了如下调查问卷,在东方广场随机调查了部分吸烟人群,并将调查结果绘制成如图所示的统计图.