题目内容
17.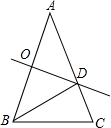 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )| A. | BD平分∠ABC | B. | ∠C=2∠A | C. | AB=CD+BC | D. | S△BCD=S△BOD |
分析 求出∠C的度数即可判断B;求出∠ABC和∠ABD的度数,求出∠DBC的度数,即可判断A;根据A、B求出的角的度数即可判断C;根据三角形面积即可判断D.
解答 解:B、∵∠A=36°,AB=AC,
∴∠C=∠ABC=72°,
∴∠C=2∠A,答案正确.
A、∵DO是AB垂直平分线,
∴AD=BD,
∴∠A=∠ABD=36°,
∴∠DBC=72°-36°=36°=∠ABD,
∴BD是∠ABC的角平分线,答案正确.
C、由A、B选项可以知道△ABC、△BDC、△ADB是等腰三角形,
∴CD+BC=CD+BD=CD+AD=AC=AB,
答案正确.
D、根据已知不能推出△BCD的面积和△BOD面积相等,错误.
故选D.
点评 本题考查了相似三角形的性质和判定,等腰三角形性质,线段垂直平分线性质的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
7.下列函数,y随x增大而减小的是( )
| A. | y=10x | B. | y=x-1 | C. | y=-3+11x | D. | y=-2x+1 |
5.为了了解某校八年级720名学生的提中情况,从中抽查了80名学生的体重进行统计分析,以下说法正确的是( )
| A. | 这80名学生是总体的一个样本 | B. | 80名学生是样本容量 | ||
| C. | 每名学生的体重是个体 | D. | 720名学生是总体 |
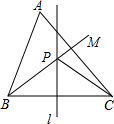 如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.
如图,锐角三角形ABC中,直线L为BC的中垂线,射线BM为∠ABC的角平分线,直线l与射线BM相交于P点,若∠A=60°,∠ACP=24°,则∠ABP的度数为32°.