题目内容
12.矩形的一组邻边长分别为4cm和3cm,它的对角线长为5cm.分析 由矩形的性质得出AC=BD,∠ABC=90°,再由勾股定理求出AC即可.
解答 解: 如图所示:
如图所示:
∵四边形ABCD是矩形,
∴AC=BD,∠ABC=90°,
∵AB=3cm,BC=4cm,
∴BD=AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{3}+{4}^{2}}$=5(cm);
故答案为:5cm.
点评 本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出AC是解决问题的关键.

练习册系列答案
相关题目
2. 如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
 如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )
如图,AB为⊙O的直径,弦CD⊥AB,E为弧BC上一点,若∠CEA=28°,则∠ABD=( )| A. | 14° | B. | 28° | C. | 56° | D. | 80° |
17.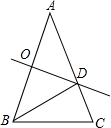 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )| A. | BD平分∠ABC | B. | ∠C=2∠A | C. | AB=CD+BC | D. | S△BCD=S△BOD |
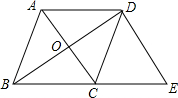 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE∥AC交BC的延长线于E.
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE∥AC交BC的延长线于E.