题目内容
2.已知菱形的两条对角线长为8和6,那么这个菱形面积是24,菱形的高$\frac{24}{5}$.分析 如图,四边形ABCD是菱形,BD=8,AC=6,作AE⊥BC于E,先利用勾股定理求出菱形边长,根据菱形的面积等于对角线乘积的一半等于底乘高,即可解决问题.
解答 解:如图,四边形ABCD是菱形,BD=8,AC=6,作AE⊥BC于E.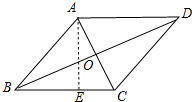
∴AC⊥BD,AO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=4,
∴AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BC=AB=5,
∴菱形的面积=$\frac{1}{2}$•AC•BD=24,
∵BC•AE=24,
∴AE=$\frac{24}{5}$,
∴菱形的高为$\frac{24}{5}$.
故答案为24,$\frac{24}{5}$.
点评 本题考查菱形的性质,记住菱形的面积的两种求法,①菱形面积等于三角形乘积的一半,②菱形的面积等于底乘高,属于基础题,中考常考题型.

练习册系列答案
相关题目
12.为了解我市八年级10000名学生的身高,从中抽取了500名学生,对其身高进行统计分析,以下说法正确的是( )
| A. | 10000名学生是总体 | B. | 本次调查采用的是普查 | ||
| C. | 样本容量是500名学生 | D. | 每个学生的身高是个体 |
17.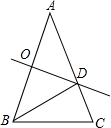 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线CD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )| A. | BD平分∠ABC | B. | ∠C=2∠A | C. | AB=CD+BC | D. | S△BCD=S△BOD |
14.已知等腰三角形的两边长为4cm和8cm,则三角形周长是( )
| A. | 12 cm | B. | 16cm | C. | 20cm | D. | 16cm或20cm |
11.下列分解因式正确的是( )
| A. | 2x2+4xy=x(2x+4y) | B. | 4a2-4ab+b2=(2a-b)2 | ||
| C. | x3-x=x(x2-1) | D. | 3x2-5xy+x=x(3x-5y) |
12. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于(1,0)及(x1,0),且-2<x1<-1,与y轴的交点在(0,2)上方,则下列结论中错误的是( )| A. | abc>0 | B. | a+b+c=0 | C. | 2a-b>-1 | D. | 2a+c<0 |
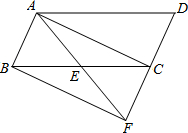 如图,在平行四边形ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.
如图,在平行四边形ABCD中,E是BC的中点,连结AE并延长,交DC的延长线于点F.