题目内容
19. 如图,在△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交 AC于点F.BE=4,CF=3,则EF=7.
如图,在△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交 AC于点F.BE=4,CF=3,则EF=7.
分析 根据角平分线定义和平行线性质求出∠EDB=∠EBD,推出DE=BE,同理得出CF=DF,即可求出答案.
解答 证明:∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵EF∥BC,
∴∠EDB=∠DBC,
∴∠EDB=∠EBD,
∴DE=BE,
同理CF=DF,
∴EF=DE+DF=BE+CF=7,
故答案为:7.
点评 本题主要考查等腰三角形的判定,掌握等角对等边是解题的关键,注意平行线的性质的应用.

练习册系列答案
相关题目
7.下列说法中正确的是( )
| A. | 平分弦的直径平分弦所对的弧 | |
| B. | 圆内接正六边形,一条边所对的圆周角是30° | |
| C. | 相等的圆周角所对的弧也相等 | |
| D. | 若两条平行直线被一个圆截得的线段长度相等,则圆心到这两条直线的距离相等 |
11.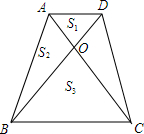 如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )
如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )
 如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )
如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )| A. | 无法确定 | B. | S1+S3<2S2 | C. | S1+S3=2S2 | D. | S1+S3>2S2 |
9.已知一元二次方程ax2+c=0(a≠0),若方程有解,则必须有c等于( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 不能确定 |
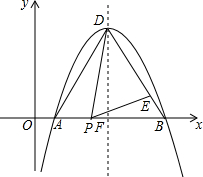 已知,在平面直角坐标系中,二次函数y=-$\frac{4}{9}$(x-4)2+4与x轴交于A、B两点,D为抛物线的顶点,对称轴与x轴交于点F,E为BD上一点,且BE:BD=1:5,P为AB上一点,且∠DPE=∠DAB,求P点坐标.
已知,在平面直角坐标系中,二次函数y=-$\frac{4}{9}$(x-4)2+4与x轴交于A、B两点,D为抛物线的顶点,对称轴与x轴交于点F,E为BD上一点,且BE:BD=1:5,P为AB上一点,且∠DPE=∠DAB,求P点坐标.