��Ŀ����
19��������C1��y1=-$\sqrt{3}$x2+2$\sqrt{3}$x�Ķ���ΪA����x��������ύ�ڵ�B���������A��B�����ꣻ
������ֱ��y2=$\sqrt{3}$x+m��������xȡ����ֵͬʱ������y2��y1����m�ķ�Χ��
����������C1�ϵĵ㣨x��y����Ϊ��kx��ky����|k|��1�����任��õ�����������C2��������C2�Ķ���ΪC����P��������C2�ϣ�����S��PBC=S��ABC���ҡ�ACP=90�㣮
�ٵ�k��1ʱ����k��ֵ��
�ڵ�k��-1ʱ������ֱ��д��k��ֵ������˵�����ɣ�
���� ���Ѻ�������ʽ��Ϊ����ʽ���ɵõ�A��1��$\sqrt{3}$�����ⷽ�̼��ɵõ�B��2��0����
������y1=-$\sqrt{3}$x2+2$\sqrt{3}$x�������£���������ΪA��1��$\sqrt{3}$����������xȡ����ֵͬʱ������y2��y1���õ�ֱ��y2=$\sqrt{3}$x+m��������y1=-$\sqrt{3}$x2+2$\sqrt{3}$x���㣬���ǵõ���=��$\sqrt{3}$��2-4$\sqrt{3}$m��0�����ɲ���ʽ���ɵõ����ۣ�
������ͼ1�У���k��1ʱ���루1��ͬ���ɵ�������C2�Ľ���ʽΪy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x������C�����꣬����S��PAC=S��ABC֪BP��AC���̶��ɵá�ABO�DZ߳�Ϊ2���������Σ��ı���CEBP�Ǿ��Σ���ʾ����P�����꣬������뵽������C2����ʽ�����k��ֵ��
����ͼ2�У���k��-1ʱ������ABO����y��ԳƵġ�A��B��O��OE���A��B�䣬ͬ���ɵ��ı���CEBP�Ǿ��Σ������������C2����ʽ����ʾ����P�����꣬������뵽������C2����ʽ�����k��ֵ��
��� �⣺����y1=-$\sqrt{3}$x2+2$\sqrt{3}$x=-$\sqrt{3}$��x-1��2+$\sqrt{3}$��
��A��1��$\sqrt{3}$����
��y1=0ʱ����-$\sqrt{3}$x2+2$\sqrt{3}$x=0��
��x1=0��x2=2��
��B��2��0����
����y1=-$\sqrt{3}$x2+2$\sqrt{3}$x�������£���������ΪA��1��$\sqrt{3}$����
������xȡ����ֵͬʱ������y2��y1��
��ֱ��y2=$\sqrt{3}$x+m��������y1=-$\sqrt{3}$x2+2$\sqrt{3}$x���㣬
��$\sqrt{3}$x+m=-$\sqrt{3}$x2+2$\sqrt{3}$x��ʵ������
���=��$\sqrt{3}$��2-4$\sqrt{3}$m��0��
��m��$\frac{\sqrt{3}}{4}$��
��m�ķ�Χ��m��$\frac{\sqrt{3}}{4}$��
������ͼ1�У���k��1ʱ��
��������C2����ԭ��O����k��$\sqrt{3}$k������2k��0�����㣬
��������C2�Ľ���ʽΪy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x��
��O��A��C���㹲�ߣ��Ҷ���CΪ��k��$\sqrt{3}$k����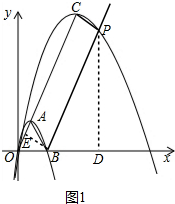
��ͼ����S��PAC=S��ABC��
��BP��AC��
����P��PD��x����D������B��BE��AO��E��
������֪��ABO�DZ߳�Ϊ2���������Σ��ı���CEBP�Ǿ��Σ�
��OE=1��CE=BP=2k-1��
�ߡ�PBD=60�㣬
��BD=k-$\frac{1}{2}$��PD=$\frac{\sqrt{3}}{2}$��2k-1����
��P��k+$\frac{3}{2}$��$\frac{\sqrt{3}}{2}$��2k-1������
��$\frac{\sqrt{3}}{2}$��2k-1��=-$\frac{\sqrt{3}}{2}$��k+$\frac{3}{2}$��2+2$\sqrt{3}$��k+$\frac{3}{2}$����
��ã�k=$\frac{9}{2}$��
����ͼ2�У���k��-1ʱ��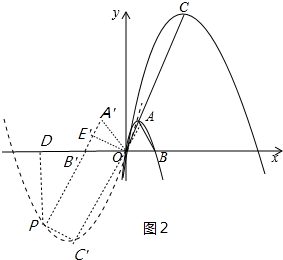
��������C2����ԭ��O����k��$\sqrt{3}$k������2k��0�����㣬
��������C2�Ľ���ʽΪy=-$\frac{\sqrt{3}}{k}$x2+2$\sqrt{3}$x��
��O��A��C�����㹲�ߣ��Ҷ���C��Ϊ��k��$\sqrt{3}$k����
����ABO����y��ԳƵġ�A��B��O��OE���A��B�䣬
��S��PAC��=S��ABC=S��AC��B����
��A��P��AC�䣬�������ı���PC��OE���Ǿ��Σ�
��PE��=OC��=-2k��B��E��=1��PB��=-2k-1��
��Rt��PDB���У��ߡ�PDB��=90�㣬��PB��D=��A��B��O=60�㣬
��DB��=$\frac{1}{2}$PB��=$\frac{12k-1}{2}$��DP=$\frac{\sqrt{3}}{2}$��-2k-1����
���P����[$\frac{2k-3}{2}$��$\frac{\sqrt{3}}{2}$��2k+1��]��
��$\frac{\sqrt{3}}{2}$��2k+1��=-$\frac{\sqrt{3}}{k}$��$\frac{2k-3}{2}$��2+2$\sqrt{3}$��$\frac{2k-3}{2}$��
��k=-$\frac{9}{2}$��
���� ������Ҫ�������ϵ����������ʽ�����κ��������ʡ���ֱ�������ε�֪ʶ�㣬���������ʾ����P�������ǽ���Ĺؼ���ѧ�����Ӹ����߹��������ı��ν�����⣬�����п�ѹ���⣮

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�| ��Ʊ���� | 1��49�� | 50��100�� | 100������ |
| ÿ����Ʊ�� | 130Ԫ | 110Ԫ | 90Ԫ |
��1�������������Ź��ж����ˣ�
��2�����������ŷֱ�Ʊ���ܼ�Ӧ����Ʊ13140Ԫ�����ʼף������������Ÿ��ж����ˣ�
��1���۲�ͼ����д�±���
| �����������ڣ� | 2 | 3 | 4 |
| �������ȣ�cm�� | 4.2 | 5.9 | 7.6 |
��3�����һ��ij���ͺ����г�����������װǰ����80��������������ɣ���ô�������������ӣ���װ�����г��ϣ����ܳ����Ƕ���cm��

| A�� | -2 | B�� | 1 | C�� | 0 | D�� | 3 |
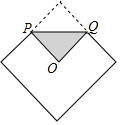 ���߳�Ϊ1�������ν���һ���۵��������ε�����λ�ã��ۺ�PQ�ij�Ϊ��������
���߳�Ϊ1�������ν���һ���۵��������ε�����λ�ã��ۺ�PQ�ij�Ϊ��������| A�� | 1 | B�� | 2 | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\sqrt{2}$ |
 ��ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CE=2DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����EG=DE+BG����AG��CF����S��FGC=3.6��������ȷ�����Ǣ٢ڢۢܢݣ�
��ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CE=2DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����EG=DE+BG����AG��CF����S��FGC=3.6��������ȷ�����Ǣ٢ڢۢܢݣ�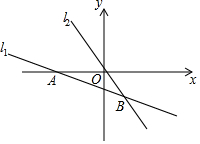 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=-$\frac{1}{2}$x+b��ֱ��l2��y=kx�ཻ�ڵ�B��m��-4������ֱ��l1��x�ύ�ڵ�A��-6��0����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��y=-$\frac{1}{2}$x+b��ֱ��l2��y=kx�ཻ�ڵ�B��m��-4������ֱ��l1��x�ύ�ڵ�A��-6��0���� ��֪����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+x�ĶԳ���Ϊֱ��x=2������ΪA����PΪ�����߶Գ�����һ�㣬����OA��OP����OA��OPʱ��P������Ϊ��2��-4����
��֪����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+x�ĶԳ���Ϊֱ��x=2������ΪA����PΪ�����߶Գ�����һ�㣬����OA��OP����OA��OPʱ��P������Ϊ��2��-4����