题目内容
7.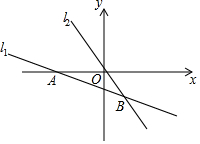 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(m,-4),且直线l1与x轴交于点A(-6,0).
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(m,-4),且直线l1与x轴交于点A(-6,0).(1)求k的值;
(2)过动点P(a,0)且垂于x轴的直线与l1、l2的交点分别为M、N,当点M位于点N上方时,请直接写出a的取值范围.
分析 (1)由待定系数法即可求得结论;
(2)由于直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(2,-4),点M位于点N上方时,即-$\frac{1}{2}$x+b>kx,观察图象可得结论.
解答 解:(1)∵直线l1:y=-$\frac{1}{2}$x+b过点A(-6,0),
∴-$\frac{1}{2}$×(-6)+b=0,解得:b=-3,
∴直线l1的函数表达式为y=-$\frac{1}{2}$x-3,
∵直线l1过点B(m,-4),
∴-$\frac{1}{2}$m-3=-4,
解得:m=2,
∵直线l2:y=kx过点B(2,-4),
∴2k=-4,
解得:k=-2;
(2)由(1)知直线l1:y=-$\frac{1}{2}$x+b与直线l2:y=kx相交于点B(2,-4),点M位于点N上方时,
即-$\frac{1}{2}$x+b>kx,
由图象得:a>2.
点评 本题考查了待定系数法求一次函数解析式,一次函数与一元一次不等式的,结合图象,比较函数图象的高低(即比较函数值的大小),确定对应的自变量的取值范围.解题的关键是掌握数形结合的思想.

练习册系列答案
相关题目
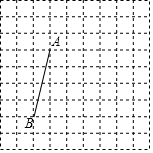 如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.