题目内容
10.已知关于x的方程x2-mx-3x+m-4=0(m为常数).(1)求证:方程有两个不相等的实数根;
(2)设x1,x2是方程的两个实数根,求(x1-1)(x2-1)的值.
分析 (1)将原方程变形为一般式,代入系数求出△=(m+1)2+24>0,由此即可证出结论;
(2)由根与系数的关系得出“x1+x2=m+3,x1•x2=m-4”,再将(x1-1)(x2-1)变形成含x1+x2和x1•x2的形式,代入数据即可得出结论.
解答 (1)证明:∵关于x的方程x2-mx-3x+m-4=0,
∴此方程为x2-(m+3)x+m-4=0,
∴△=[-(m+3)]2-4(m-4)=m2+2m+25=(m+1)2+24,
∴△>0,
∴关于x的方程x2-mx-3x+m-4=0有两个不相等的实数根.
(2)解:∵x1,x2是方程的两个实数根,
∴x1+x2=-$\frac{b}{a}$=m+3,x1•x2=$\frac{c}{a}$=m-4,
∴(x1-1)(x2-1)=x1•x2-(x1+x2)+1=(m-4)-(m+3)+1=-6.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是:(1)找出△=(m+1)2+24>0;(2)结合根与系数的关系找出x1+x2=m+3,x1•x2=m-4.本题属于基础题,难度不大,解决该题型题目时,由根的判别式的符号来判断方程根的个数是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
5. 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
 如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
如图,在直角坐标系xOy中,A(-4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )| A. | (1,$\frac{5}{2}$) | B. | ($\frac{4}{3}$,$\frac{8}{3}$) | C. | ($\sqrt{5}$,2$\sqrt{5}$) | D. | ($\sqrt{3}$,2$\sqrt{3}$) |
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 正方形 | D. | 圆 |
19.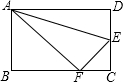 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | 5 |
20.下列各式正确的是( )
| A. | 20=0 | B. | |-$\sqrt{2}$|=$\sqrt{2}$ | C. | $\sqrt{4}$=±2 | D. | -22=4 |
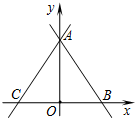 如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.
如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.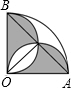 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)