Question

19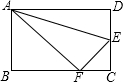．如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，则tan∠EAF的值是（　　）

• A． $\frac{1}{2}$
• B． $\frac{3}{4}$
• C． 2
• D． 5

Answer 1

分析 先根据矩形的性质得CD=AB=8，AD=BC=10，再根据折叠的性质得AF=AD=10，DE=EF，∠AFE=∠D=90°，在Rt△ABF中，利用勾股定理计算出BF=6，则FC=BC-BF=4，设EF=x，则DE=x，CE=CD-DE=8-x，在Rt△CEF中，根据勾股定理得到4²+（8-x）²=x²，解得x=5，即EF=5，然后在Rt△AEF中根据正切的定义求解．

解答 解：∵四边形ABCD为矩形，
∴CD=AB=8，AD=BC=10，
∵折叠矩形ABCD的一边AD，使点D落在BC边的点F处，
∴AF=AD=10，DE=EF，∠AFE=∠D=90°，
在Rt△ABF中，BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=6，
∴FC=BC-BF=4，
设EF=x，则DE=x，CE=CD-DE=8-x，
在Rt△CEF中，
∵CF²+CE²=EF²，
∴4²+（8-x）²=x²，
解得：x=5，
∴EF=5，
在Rt△AEF中，tan∠EAF=$\frac{EF}{AF}$=$\frac{5}{10}$=$\frac{1}{2}$；
故选：A．

点评 本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了矩形的性质和勾股定理．