题目内容
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
考点:二次函数的应用
专题:
分析:(1)根据进价为每件40元,售价为每件50元,每个月可卖出210件,再根据每件商品的售价每上涨1元,则每个月少卖10件和销售利润=件数×每件的利润列出关系式,即可得出答案.
(2)根据(1)得出的函数关系式,再进行配方得出y=-10(x-5.5)2+2402.5,当x=5.5时y有最大值,从而得出答案.
(2)根据(1)得出的函数关系式,再进行配方得出y=-10(x-5.5)2+2402.5,当x=5.5时y有最大值,从而得出答案.
解答:解:(1)由题意得:y=(210-10x)(50+x-40)
=-10x2+110x+2100(0<x≤15且x为整数);
(2)根据(1)得:
y=-10x2+110x+2100,
y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
=-10x2+110x+2100(0<x≤15且x为整数);
(2)根据(1)得:
y=-10x2+110x+2100,
y=-10(x-5.5)2+2402.5,
∵a=-10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),
当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
点评:本题考查二次函数的实际应用,关键是读懂题意,找出之间的等量关系,根据每天的利润=一件的利润×销售件数,建立函数关系式,此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
n3+100能被n+10整除的正整数n的最大值是( )
| A、90 | B、890 |
| C、900 | D、990 |
在一次射击中,甲、乙两人5次射击的成绩分别如下:(单位:环)
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
甲:10,8,10,10,7 乙:7,9,9,10,10
这次射击中,甲、乙二人方差大小关系为( )
A、S
| ||||
B、S
| ||||
C、S
| ||||
| D、无法确定 |
 如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.
如图所示,是由几个小立方块所搭几何体的俯视图,小立方块中的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.
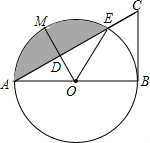 如图,以线段AB为直径的⊙O交线段AC于点E,点M是
如图,以线段AB为直径的⊙O交线段AC于点E,点M是