题目内容
规定对于一个一次函数,如果它的自变量x与函数值y满足m≤x≤n时有m≤y≤n,我们称此函数为为区间[m,n]上的闭函数.
(1)判断y=-x+5是否为[2,3]上的闭函数;
(2)若一次函数y=kx+b是[-3,4]的闭函数,求此函数解析式.
(1)判断y=-x+5是否为[2,3]上的闭函数;
(2)若一次函数y=kx+b是[-3,4]的闭函数,求此函数解析式.
考点:一次函数的性质
专题:新定义
分析:(1)分别计算出自变量为2或3时的函数值,然后根据闭函数的定义进行判断;
(2)根据闭函数的定义得到当x=-3时,y=-3,当x=4时,y=4或当x=-3时,y=4,当x=4时,y=-3,然后利用待定系数法求出两种情况下的解析式.
(2)根据闭函数的定义得到当x=-3时,y=-3,当x=4时,y=4或当x=-3时,y=4,当x=4时,y=-3,然后利用待定系数法求出两种情况下的解析式.
解答:解:(1)x=2时,y=-x+5=3;当x=3时,y=-x+5=2,
所以y=-x+5为[2,3]上的闭函数;
(2)当x=-3时,y=-3,当x=4时,y=4,所以
,解得
,此时函数解析式为y=x;
当x=-3时,y=4,当x=4时,y=-3,所以
,解得
,此时函数解析式为y=-x+1,
所以所求函数解析式为y=x或y=-x+1.
所以y=-x+5为[2,3]上的闭函数;
(2)当x=-3时,y=-3,当x=4时,y=4,所以
|
|
当x=-3时,y=4,当x=4时,y=-3,所以
|
|
所以所求函数解析式为y=x或y=-x+1.
点评:本题考查了一次函数的性质:k>0,y随x的增大而增大,函数从左到右上升;k<0,y随x的增大而减小,函数从左到右下降.

练习册系列答案
相关题目




 如图A,B两点的坐标分别是(2,-1),(2,1),你能确定(3,3)的位置吗?
如图A,B两点的坐标分别是(2,-1),(2,1),你能确定(3,3)的位置吗?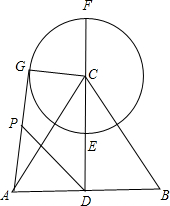 如图,在△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径作⊙C,点G是⊙C上的一个动点,P是AG中点,DP的最大值为多少?
如图,在△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径作⊙C,点G是⊙C上的一个动点,P是AG中点,DP的最大值为多少?