题目内容
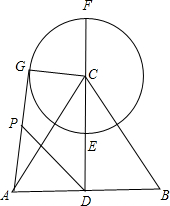 如图,在△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径作⊙C,点G是⊙C上的一个动点,P是AG中点,DP的最大值为多少?
如图,在△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径作⊙C,点G是⊙C上的一个动点,P是AG中点,DP的最大值为多少?考点:圆的综合题,线段的性质:两点之间线段最短,等腰三角形的性质,勾股定理,三角形中位线定理
专题:
分析:根据等腰三角形的性质可得点D是AB的中点,然后根据三角形中位线定理可得DP=
BG,然后利用两点之间线段最短就可解决问题.
| 1 |
| 2 |
解答:解:连接BG,如图.
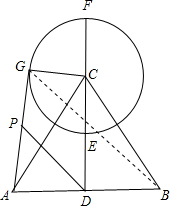
∵CA=CB,CD⊥AB,AB=6,
∴AD=BD=
AB=3.
又∵CD=4,
∴BC=5.
∵E是高线CD的中点,
∴CE=
CD=2,
∴CG=CE=2.
根据两点之间线段最短可得:BG≤CG+CB=2+5=7.
当B、C、G三点共线时,BG取最大值为7.
∵P是AG中点,D是AB的中点,
∴PD=
BG,
∴DP最大值为
.

∵CA=CB,CD⊥AB,AB=6,
∴AD=BD=
| 1 |
| 2 |
又∵CD=4,
∴BC=5.
∵E是高线CD的中点,
∴CE=
| 1 |
| 2 |
∴CG=CE=2.
根据两点之间线段最短可得:BG≤CG+CB=2+5=7.
当B、C、G三点共线时,BG取最大值为7.
∵P是AG中点,D是AB的中点,
∴PD=
| 1 |
| 2 |
∴DP最大值为
| 7 |
| 2 |
点评:本题主要考查了等腰三角形的性质、三角形中位线定理、勾股定理、两点之间线段最短等知识,利用三角形中位线定理将DP转化为BG是解决本题的关键.

练习册系列答案
相关题目
小静在甲商场用38.4元买了若干瓶酸奶,后来她发现同样的酸奶在乙商场比甲商场每瓶便宜0.2元,于是她在乙商场花了54元买了一批酸奶,并且买的瓶数比第一次买的瓶数多
倍,问小静在甲商场买了多少瓶酸奶?
| 1 |
| 2 |
下列函数中,反比例函数是( )
| A、y=x-1 | ||
B、y=
| ||
C、y=
| ||
D、y=
|