题目内容
14.在今年“五•一”小长假期间,某学校团委要求学生参加一项社会调查活动,八年级学生小明想了解他所居住的小区500户居民的家庭收入情况,从中随机调查了本小区一定数量居民家庭的收入情况(收入取整数,单位:元),并将调查的数据绘制成如下直方图和扇形图,根据图中提供的信息,解答下列问题:
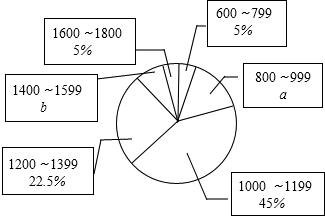
(1)这次共调查了40个家庭的收入,a=15%,b=7.5%;
(2)补全频数分布直方图,样本的中位数落在第三个小组;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
(4)在第1组和第5组的家庭中,随机抽取2户家庭,求这两户家庭人均月收入差距不超过200元的概率.
分析 (1)用第1组的频数除以它所占百分比即可得到调查的总家庭数,再用第2组的频数除以总家庭数得到a的值,接着计算出第3组的频数,然后计算出第5组的频数,再计算出b的值;
(2)根据中位数的定义可判断样本的中位数落在第3个小组;然后补全频数分布直方图;
(3)用500乘以前面2组的频率和即可估计该居民小区家庭收入较低(不足1000元)的户数;
(4)设第1组的2户用A、B表示,第5组的3户用a、b、c表示,画树状图展示所有20种等可能的结果数,再找出这两户家庭人均月收入差距不超过200元的结果数,然后根据概率公式计算.
解答 解:(1)2÷5%=40(个),所以这次共调查了40个家庭;
a=6÷40=15%,
第三组的家庭个数=40×45%=18(个),
b=(40-2-6-18-9-2)÷40=7.5%,
(2)第20个数和第21个数都落在第三组,所以样本的中位数落在第三个小组,
如图,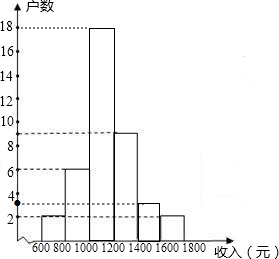
故答案为40,15%,7.5%;三;
(3)500×(5%+15%)=100(户),
所以估计该居民小区家庭收入较低(不足1000元)的户数大约有100户;
(4)设第1组的2户用A、B表示,第5组的3户用a、b、c表示,
画树状图为:
共有20种等可能的结果数,其中这两户家庭人均月收入差距不超过200元的结果数为8,
所以这两户家庭人均月收入差距不超过200元的概率=$\frac{8}{20}$=$\frac{2}{5}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图和用样本估计总体.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
2.某校男子足球队队员的年龄分布如表所示:
则这些队员年龄的中位数是15岁.
| 年龄(岁) | 13 | 14 | 15 | 16 | 17 |
| 人数 | 2 | 6 | 8 | 3 | 3 |
4.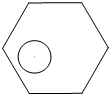 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )| A. | a2(2$\sqrt{3}$-aπ) | B. | r2(2π-$\sqrt{3}$) | C. | a2r2(2$\sqrt{3}$-π) | D. | r2(2$\sqrt{3}$-π) |
 如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)
如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)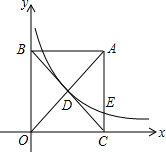 如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x.
如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x. 二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)
二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)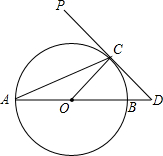 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.