题目内容
4.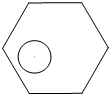 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )| A. | a2(2$\sqrt{3}$-aπ) | B. | r2(2π-$\sqrt{3}$) | C. | a2r2(2$\sqrt{3}$-π) | D. | r2(2$\sqrt{3}$-π) |
分析 当⊙O运动到正六边形的角上时,圆与∠ABC两边的切点分别为E,F,连接OE,OF,OB,根据正六边形的性质可知∠ABC=120°,故∠OBF=60°,再由锐角三角函数的定义用r表示出BF的长,可知圆形纸片不能接触到的部分的面积=6×2S△BOF-S扇形EOF,由此可得出结论.
解答 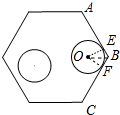 解:如图所示,连接OE,OF,OB,
解:如图所示,连接OE,OF,OB,
∵此多边形是正六边形,
∴∠ABC=120°,
∴∠OBF=60°.
∵∠OFB=90°,OF=r,
∴BF=$\frac{OF}{tan60°}$=$\frac{\sqrt{3}}{3}$r,
∴圆形纸片不能接触到的部分的面积
=6×2S△BOF-6S扇形EOF
=6×2×$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$r•r-6×$\frac{60π•{r}^{2}}{360}$
=r2(2$\sqrt{3}$-π).
故选D.
点评 本题考查的是正多边形和圆,熟知正六边形的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
 如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )| A. | 20 | B. | 25 | C. | 30 | D. | 35 |

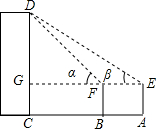 某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗?
某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗?