题目内容
19. 二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)
二七纪念塔是我省郑州市的标志性建筑,某兴趣小组为了测量二七纪念塔的高度,进行了如下的研究.如图,AB为二七纪念塔,从地面C点看塔顶A点,仰角为45°,到建筑DE顶端E点后,从E点看塔顶A点,仰角为60°,C、D、B三点在同一直线上.已知建筑DE高度为35.3米,∠ECD=37°,求二七纪念塔AB的高度.(结果保留整数,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;$\sqrt{3}$≈1.732)
分析 根据题意得出BF=DE=35.3米,BD=EF,∠AFE=∠CDE=90°,设EF=BD=x米,由三角函数求出CD的长,BA=BC,得出方程,解方程求出EF,得出AF,即可得出结果.
解答 解:根据题意得:BF=DE=35.3米,BD=EF,∠AFE=∠CDE=90°,
设EF=BD=x米,
∵∠AEF=60°,∠ECD=37°,
∴AF=$\sqrt{3}$EF,CD=$\frac{DE}{tan37°}$=$\frac{35.3}{0.75}$≈47.07米,
∵∠ABC=90°,∠ACB=45°,
∴BA=BC,即$\sqrt{3}$x+35.3=47.06+x,
解得:x=16.07,sy5AF=$\sqrt{3}$≈27.83(米),
∴AB=AF+BF=27.83+35.3≈63(米);
答:二七纪念塔AB的高度为63米.
点评 本题考查了解直角三角形-仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形;通过解直角三角形得出方程是解决问题的关键.

练习册系列答案
相关题目
10.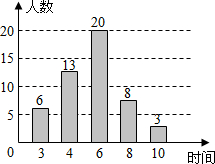 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
8.小明和小杰为了估计抛掷图钉时针尖朝上的概率,分别做了试验.小明的试验结果记录在表一,小杰的试验结果记录在表二.
表一:
表二:
(1)在小明的试验中,针尖朝上的频率是多少?在小杰的试验中,针尖朝上的频率又是多少?
(2)求针尖朝上的概率估计值,并说明理由.
表一:
| 试验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 针尖朝上次数 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 |
| 试验次数 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 针尖朝上次数 | 6 | 13 | 18 | 25 | 34 | 40 | 45 | 52 | 58 | 65 |
(2)求针尖朝上的概率估计值,并说明理由.