题目内容
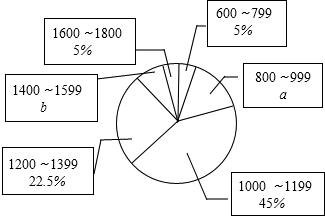
5. 如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)
如图,河岸BD北侧有两个村庄A、C,C村庄到河岸的距离CD为300米,此时,A村庄在河岸D处的西北方向,在C村庄的北偏西60°方向上,求两村庄之间的距离AC.(结果保留整数,参考数据:$\sqrt{2}≈1.414,\sqrt{3}≈1.732$)
分析 作AE⊥DC于E,在Rt△ACE中,解直角三角形得出AC=2CE,AE=$\sqrt{3}$CE,设CE=x,则AC=2x,AE=$\sqrt{3}$x,在Rt△ADE中,证出AE=DE,得出方程,解方程求出CE,即可得出AC.
解答 解:作AE⊥DC于E,如图所示:
在Rt△ACE中,∵∠ACE=60°,
∴∠CAE=30°,
∴AC=2CE,AE=$\sqrt{3}$CE,
设CE=x,则AC=2x,AE=$\sqrt{3}$x,
在Rt△ADE中,DE=CE+CD=x+300,∠ADE=45°,
∴AE=DE,即$\sqrt{3}$x=x+300,
解得:x=150($\sqrt{3}$+1),
∴AC=2CE=300($\sqrt{3}$+1)≈820(米);
答:两村庄之间的距离AC约为820米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据方向角构造直角三角形,根据题意得出方程是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
16.a与$\frac{1}{3}$互为相反数,则a的倒数是( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
13.不等式1-2x>3的解集是( )
| A. | x>1 | B. | x>-1 | C. | x<1 | D. | x<-1 |
10.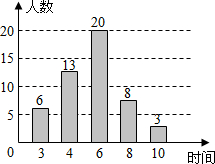 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
 小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )
小明对居住在某小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图,这组数据的众数和中位数分别是( )| A. | 6,4 | B. | 6,6 | C. | 4,4 | D. | 4,6 |
17.下列事件中,属于随机事件的是( )
| A. | 测量某天的最高气温是100℃ | |
| B. | 度量四边形的内角和,结果是360° | |
| C. | 掷一枚骰子,向上一面的数字是2 | |
| D. | 袋中装有5只黑球,从中摸出一个是黑球 |
 某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)
某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,$\sqrt{2}≈1.4,\sqrt{3}≈1.7$)