题目内容
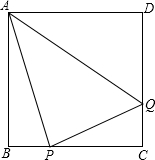 如图,在边长为4的正方形ABCD中,动点P从点B出发沿BC向点C运动,动点Q同时以相同的速度从点C出发沿CD向D点运动.
如图,在边长为4的正方形ABCD中,动点P从点B出发沿BC向点C运动,动点Q同时以相同的速度从点C出发沿CD向D点运动.(1)设BP=x,当x为何值时三角形△APQ面积最小,求出最小值;
(2)探究:△APQ能否构成直角三角形?若能,请确定点P所有可能的位置;若不能,请说明理由.
考点:四边形综合题
专题:综合题
分析:(1)根据正方形的性质表示出PC=4-x,DQ=4-x,再利用三角形面积公式和S△APQ=S正方形ABCD-S△ABP-S△PCQ-S△ADQ进行计算得到S△APQ=
x2-2x+8,然后配方后利用二次函数的性质求解;
(2)根据勾股定理,在Rt△ABP中得到AP2=AB2+BP2=42+x2,在Rt△PCQ中得到PQ2=CQ2+PC2=x2+(4-x)2=2x2-8x+16,在Rt△ADQ中得到AQ2=AD2+DQ2=42+(4-x)2=x2-8x+32,然后分类讨论:当∠APQ=90°时,根据勾股定理得42+x2+2x2-8x+16=x2-8x+32;当∠AQP=90°时,根据勾股定理得到42+x2=2x2-8x+16+x2-8x+32;当∠PAQ=90°时,根据勾股定理得到即42+x2+x2-8x+32=2x2-8x+16,然后分别解方程求出x的值,从而得到P点的位置.
| 1 |
| 2 |
(2)根据勾股定理,在Rt△ABP中得到AP2=AB2+BP2=42+x2,在Rt△PCQ中得到PQ2=CQ2+PC2=x2+(4-x)2=2x2-8x+16,在Rt△ADQ中得到AQ2=AD2+DQ2=42+(4-x)2=x2-8x+32,然后分类讨论:当∠APQ=90°时,根据勾股定理得42+x2+2x2-8x+16=x2-8x+32;当∠AQP=90°时,根据勾股定理得到42+x2=2x2-8x+16+x2-8x+32;当∠PAQ=90°时,根据勾股定理得到即42+x2+x2-8x+32=2x2-8x+16,然后分别解方程求出x的值,从而得到P点的位置.
解答:解:(1)∵BP=x(0≤x≤4),
∴CQ=x,PC=4-x,DQ=4-x,
∵S△APQ=S正方形ABCD-S△ABP-S△PCQ-S△ADQ
=4•4-
•4•x-
•x•(4-x)-
•4•(4-x)
=
x2-2x+8
=
(x-2)2+6,
∴当x=2时,S△APQ有最小值,最小值为6;
(2)能.
在Rt△ABP中,AP2=AB2+BP2=42+x2,
在Rt△PCQ中,PQ2=CQ2+PC2=x2+(4-x)2=2x2-8x+16,
在Rt△ADQ中,AQ2=AD2+DQ2=42+(4-x)2=x2-8x+32,
当∠APQ=90°时,则AP2+PQ2=AQ2,即42+x2+2x2-8x+16=x2-8x+32,
整理得x2=0,解得x=0,
∴此时P点在B点处,
当∠AQP=90°时,则AP2=PQ2+AQ2,即42+x2=2x2-8x+16+x2-8x+32,
整理得x2-8x+16=0,解得x=4,
∴此时P点在C点处;
当∠PAQ=90°时,则AP2+AQ2=PQ2,即42+x2+x2-8x+32=2x2-8x+16,
此方程无解.
综上所述,当点P在B点或C点时,△APQ为直角三角形.
∴CQ=x,PC=4-x,DQ=4-x,
∵S△APQ=S正方形ABCD-S△ABP-S△PCQ-S△ADQ
=4•4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴当x=2时,S△APQ有最小值,最小值为6;
(2)能.
在Rt△ABP中,AP2=AB2+BP2=42+x2,
在Rt△PCQ中,PQ2=CQ2+PC2=x2+(4-x)2=2x2-8x+16,
在Rt△ADQ中,AQ2=AD2+DQ2=42+(4-x)2=x2-8x+32,
当∠APQ=90°时,则AP2+PQ2=AQ2,即42+x2+2x2-8x+16=x2-8x+32,
整理得x2=0,解得x=0,
∴此时P点在B点处,
当∠AQP=90°时,则AP2=PQ2+AQ2,即42+x2=2x2-8x+16+x2-8x+32,
整理得x2-8x+16=0,解得x=4,
∴此时P点在C点处;
当∠PAQ=90°时,则AP2+AQ2=PQ2,即42+x2+x2-8x+32=2x2-8x+16,
此方程无解.
综上所述,当点P在B点或C点时,△APQ为直角三角形.
点评:本题考查了四边形的综合题:熟练掌握正方形的性质和二次函数的性质;会运用勾股定理表示线段之间的关系;会运用分类讨论思想的解决数学问题.

练习册系列答案
相关题目
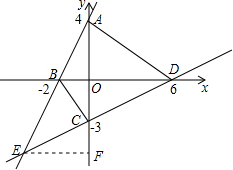 已知直线m经过两点(1,6)、(-3,-2),它和x轴、y轴的交点式B、A,直线n过点(2,-2),且与y轴交点的纵坐标是-3,它和x轴、y轴的交点是D、C;
已知直线m经过两点(1,6)、(-3,-2),它和x轴、y轴的交点式B、A,直线n过点(2,-2),且与y轴交点的纵坐标是-3,它和x轴、y轴的交点是D、C;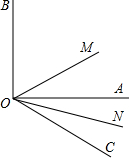 已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线.
已知:如图,ON是∠AOC的平分线,OM是∠AOB的平分线. 如图,点A、B、C是⊙O上三点,∠AOC=130°,则∠ABC=
如图,点A、B、C是⊙O上三点,∠AOC=130°,则∠ABC=