题目内容
12.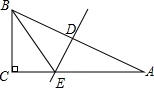 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交AC于点E,且∠EBC=3∠EBA,则∠A等于( )
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交AC于点E,且∠EBC=3∠EBA,则∠A等于( )| A. | 18° | B. | 22.5° | C. | 25° | D. | 27.5° |
分析 根据线段垂直平分线性质得出AE=BE,推出∠A=∠EBA,求出∠ABC=4∠A,根据三角形内角和定理得出5∠A=90°,即可求出答案.
解答 解:∵AB的垂直平分线交AB于点D,交AC于点E,
∴AE=BE,
∴∠A=∠EBA,
∵∠EBC=3∠EBA,
∴∠ABC=4∠A,
∵∠C=90°,
∴5∠A=90°,
∴∠A=18°,
故选A.
点评 本题考查了线段垂直平分线性质的应用,能根据性质求出AE=BE是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
2.(2+x)(x-2)的结果是( )
| A. | x2-4 | B. | 2-x2 | C. | 4+x2 | D. | 2+x2 |
3.下列各式中,最简二次根式是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{26}$ | C. | $\sqrt{0.5}$ | D. | $\frac{\sqrt{2}}{\sqrt{3}}$ |
7.给出下面四个方程及其变形,其中变形正确的是( )
①4(x+2)=0变形为x+2=0;
②x+7=5-3x变形为4x=-2;
③$\frac{2}{5}$x=3变形为2x=15;
④8x=7变形为x=$\frac{8}{7}$.
①4(x+2)=0变形为x+2=0;
②x+7=5-3x变形为4x=-2;
③$\frac{2}{5}$x=3变形为2x=15;
④8x=7变形为x=$\frac{8}{7}$.
| A. | ①③④ | B. | ①②④ | C. | ③④② | D. | ①②③ |
4.已知一个Rt△的两边长分别为3和4,则第三边长的是( )
| A. | 5 | B. | 7 | C. | $\sqrt{7}$ | D. | $\sqrt{7}$或5 |
2.计算$\frac{{x}^{2}-{y}^{2}}{xy}$-$\frac{xy-{y}^{2}}{xy-{x}^{2}}$的结果是( )
| A. | $\frac{x}{y}$ | B. | $\frac{{x}^{2}+2y}{xy}$ | C. | x2 | D. | $\frac{3x}{{x}^{2}-1}$ |
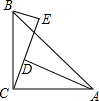 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D. 如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.
如图是一块直角三角形形状的绿地,量得两直角边长分别为6,8.现在要将绿地扩充成等腰三角形,且扩充的图形是以8长的边为直角边的直角三角形,求扩充后等腰三角形绿地的三边长的平方和.