题目内容
4.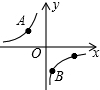 如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )| A. | (-2$\sqrt{2}$,2$\sqrt{2}$) | B. | (-1,8) | C. | (-2,4) | D. | (-4,2) |
分析 把x=1、y=-1分别代入解析式求得B、C的坐标,然后设A的坐标为(a,-$\frac{8}{a}$),根据题意,结合勾股定理列出(a-1)2+(-$\frac{8}{a}$+8)2=(a-8)2+(-$\frac{8}{a}$+1)2,解方程即可求得.
解答 解:∵A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,点B的横坐标为1,点C的纵坐标为-1,
∴B(1,-8),C(8,-1),
设A(a,-$\frac{8}{a}$),
∵△ABC是以BC为底的等腰三角形,
∴AB=AC,
∴(a-1)2+(-$\frac{8}{a}$+8)2=(a-8)2+(-$\frac{8}{a}$+1)2,
整理得,2a2=16,
∵a<0,
∴a=-2$\sqrt{2}$,
∴A的坐标为(-2$\sqrt{2}$,2$\sqrt{2}$).
故选A.
点评 本题考查了反比例函数图象上点的坐标特征,等腰三角形的性质,根据等腰三角形的性质列出方程是本题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
19.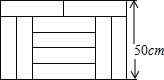 如图,宽为50厘米的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50厘米的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
 如图,宽为50厘米的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )
如图,宽为50厘米的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )| A. | 400厘米2 | B. | 500厘米2 | C. | 600厘米2 | D. | 700厘米2 |
14.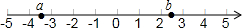 a、b在数轴上的位置如图,则下列结论正确的是( )
a、b在数轴上的位置如图,则下列结论正确的是( )
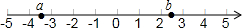 a、b在数轴上的位置如图,则下列结论正确的是( )
a、b在数轴上的位置如图,则下列结论正确的是( )| A. | a-b<0 | B. | ab>0 | C. | -a<b | D. | |a|<|b| |
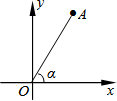 如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.
如图,点A(3,t)在第一象限,OA与x轴所夹的锐角为α,tanα=$\frac{3}{2}$,则t的值是$\frac{9}{2}$.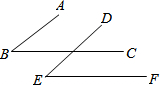 如图,已知AB∥DE,BC∥EF,∠B=35°,则∠E=35°.
如图,已知AB∥DE,BC∥EF,∠B=35°,则∠E=35°. 如图,在矩形ABCD中,对角线AC与BD相交于O,AB=6,AC=10,则AD=8.
如图,在矩形ABCD中,对角线AC与BD相交于O,AB=6,AC=10,则AD=8.