题目内容
12.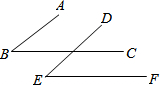 如图,已知AB∥DE,BC∥EF,∠B=35°,则∠E=35°.
如图,已知AB∥DE,BC∥EF,∠B=35°,则∠E=35°.
分析 由两直线平行同位角相等可得:∠B=∠1,∠E=∠1,进而可得:∠B=∠E,然后由∠B=35°,即可求出∠E的度数.
解答 解:如图所示,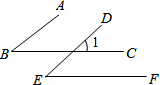
∵AB∥DE,BC∥EF,
∴∠B=∠1,∠E=∠1,
∴∠B=∠E,
∵∠B=35°,
∴∠E=35°.
故答案为:35°.
点评 此题考查了平行线的性质,解题的关键是:熟记两直线平行同位角相等,两直线平行内错角相等,两直线平行同旁内角互补.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.若a<0,b>0,则化简$\sqrt{{a}^{2}{b}^{3}}$的结果为( )
| A. | ab$\sqrt{ab}$ | B. | -ab$\sqrt{b}$ | C. | ab$\sqrt{b}$ | D. | ab2$\sqrt{b}$ |
4.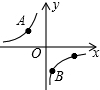 如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
 如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )| A. | (-2$\sqrt{2}$,2$\sqrt{2}$) | B. | (-1,8) | C. | (-2,4) | D. | (-4,2) |
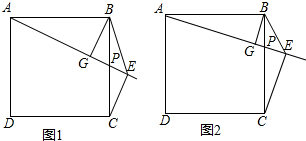
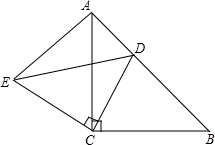 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为线段AB上一动点.