题目内容
9.若$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{1}{2}$,则$\frac{a+c+e}{b+d+f}$=$\frac{1}{2}$.分析 直接根据等比性质求解.
解答 解:∵$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{1}{2}$,
∴$\frac{a+b+c}{b+d+f}$=$\frac{a}{b}$=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查了比例的基本性质:内项之积等于外项之积;合比性质;合分比性质;等比性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若a<0,b>0,则化简$\sqrt{{a}^{2}{b}^{3}}$的结果为( )
| A. | ab$\sqrt{ab}$ | B. | -ab$\sqrt{b}$ | C. | ab$\sqrt{b}$ | D. | ab2$\sqrt{b}$ |
4.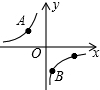 如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
 如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )
如图,A、B、C是反比例函数y=-$\frac{8}{x}$图象上的点,且△ABC是以BC为底的等腰三角形,点B的横坐标为1,点C的纵坐标为-1,则点A的坐标为( )| A. | (-2$\sqrt{2}$,2$\sqrt{2}$) | B. | (-1,8) | C. | (-2,4) | D. | (-4,2) |
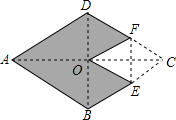 如图,菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若AC=8,BD=6,则图中阴影部分的面积为18.
如图,菱形ABCD中,AC与BD相交于点O.将菱形沿EF折叠,使点C与点O重合.若AC=8,BD=6,则图中阴影部分的面积为18. 如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{15}$,则⊙P的弦心距是1;a的值是4+$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为$2\sqrt{15}$,则⊙P的弦心距是1;a的值是4+$\sqrt{2}$.