题目内容
20.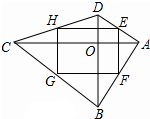 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )| A. | AC平分BD | B. | AC⊥BD | C. | AC=BD | D. | AC与BD互相平分 |
分析 根据三角形的中位线定理,可以证明所得四边形的两组对边分别和两条对角线平行,所得四边形的两组对边分别是两条对角线的一半,再根据平行四边形的判定就可证明该四边形是一个平行四边形;所得四边形要成为矩形,则需有一个角是直角,故对角线应满足互相垂直.
解答 解:如图,∵E,F分别是边AD,AB的中点,
∴EF∥BD,EF=$\frac{1}{2}$BD,
同理HG∥BD,HG=$\frac{1}{2}$BD,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形;
要使四边形EFGH是矩形,则需EF⊥FG,即AC⊥BD;
故选:B.
点评 此题主要考查了三角形的中位线定理的运用.同时熟记此题中的结论:顺次连接四边形各边中点所得四边形是平行四边形;顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.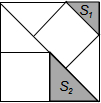 有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )
有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )
 有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )
有3个正方形按如图所示放置,其中大正方形的边长是1,阴影部分的面积依次记为S1,S2,则S1+S2等于( )| A. | $\frac{13}{72}$ | B. | $\frac{13}{36}$ | C. | $\frac{17}{72}$ | D. | $\frac{3}{16}$ |
8.下列二次根式,化简结果为-4( )
| A. | $\sqrt{(-4)^{2}}$ | B. | (-$\sqrt{4}$)2 | C. | -$\sqrt{{4}^{2}}$ | D. | $\sqrt{{4}^{2}}$ |
 (1)计算:$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2
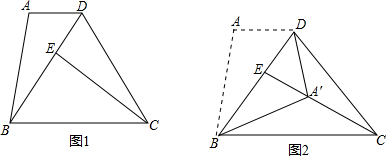
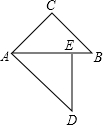
(1)计算:$\frac{5}{\sqrt{5}}$-(2-$\sqrt{5}$)0+($\frac{1}{2}$)-2 如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.
如图,△ABC中,AB=7,AC=5,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.