题目内容
15.如图1,在四边形ABCD中,AD∥BC,DB=DC=EC,∠A=2∠ADB,AD=m,AB=n.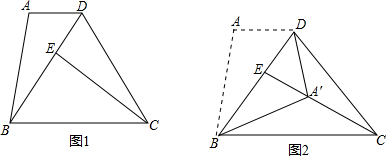
(1)在图1中找出与∠ABD相等的角,并加以证明;
(2)求BE的长;
(3)将△ABD沿BD翻折,得到△A′BD.若点A′恰好落在EC上(如图2),求$\frac{m}{n}$的值.
分析 (1)由平行线的性质知∠DBC=∠ADB,由DB=DC,得出∠DCB=∠DBC=∠ADB,由DC=EC,得出∠CDE=∠CED=∠DBC+∠BCE=∠ADB+∠BCE,再由三角形内角和定理即可得出结果;
(2)在BC上取一点F,使CF=AB=n,连接EF,由SAS证得△ABD≌△FCE,得出∠EFC=∠DAB=2∠ADB,∠FEC=∠ADB,EF=AD=m,推出∠BEF=∠EFC-∠EBC=2∠ADB-∠ADB=∠ADB=∠EBF,BF=EF=m,BC=BF+FC=m+n,再由△EBC∽△ADB,得出$\frac{BC}{DB}$=$\frac{EC}{AB}$=$\frac{BE}{DA}$,代入数值即可得出结果;
(3)由折叠性质知A′B=AB=n,∠A′BE=∠ABE,由△A′EB∽△BEC,得出$\frac{A′B}{BC}$=$\frac{BE}{CE}$=$\frac{BE}{DB}$,代入数值即可得出结果.
解答 解:(1)∠BCE=∠ABD,理由如下:
∵AD∥BC,
∴∠DBC=∠ADB,
∵DB=DC,
∴∠DCB=∠DBC=∠ADB,
∵DC=EC,
∴∠CDE=∠CED=∠DBC+∠BCE=∠ADB+∠BCE,
∵∠DBC+∠DCB+∠CDB=180°,即∠ADB+∠ADB+(∠ADB+∠BCE)=3∠ADB+∠BCE=180°,
又∵∠A+∠ABD+∠ADB=180°,∠A=2∠ADB,
∴3∠ADB+∠ABD=180°,
∴∠BCE=∠ABD;
(2)在BC上取一点F,使CF=AB=n,连接EF,如图1所示:
由(1)知:∠ABD=∠FCE,
在△ABD和△FCE中,$\left\{\begin{array}{l}{AB=CF}\\{∠ABD=∠FCE}\\{DB=EC}\end{array}\right.$,
∴△ABD≌△FCE(SAS),
∴∠EFC=∠DAB=2∠ADB,∠FEC=∠ADB,EF=AD=m,
∴∠BEF=∠EFC-∠EBC=2∠ADB-∠ADB=∠ADB=∠EBF,
∴BF=EF=m,BC=BF+FC=m+n,
∵∠EBC=∠ADB,∠BCE=∠DBA,
∴△EBC∽△ADB,
∴$\frac{BC}{DB}$=$\frac{EC}{AB}$=$\frac{BE}{DA}$,即:$\frac{m+n}{DB}$=$\frac{DB}{n}$=$\frac{BE}{m}$,
∴DB=$\sqrt{n(m+n)}$,
∴BE=$\frac{m\sqrt{n(m+n)}}{n}$;
(3)∵将△ABD沿BD翻折,得到△A′BD,点A′恰好落在EC上,
∴A′B=AB=n,∠A′BE=∠ABE,
由(1)知:∠ABE=∠BCE,
∴∠A′BE=∠BCE,
∵∠A′EB=∠BEC,
∴△A′EB∽△BEC,
∴$\frac{A′B}{BC}$=$\frac{BE}{CE}$=$\frac{BE}{DB}$,即:$\frac{n}{m+n}$=$\frac{\frac{m\sqrt{n(m+n)}}{n}}{\sqrt{n(m+n)}}$,
整理得:m2+mn-n2=0,即($\frac{m}{n}$)2+$\frac{m}{n}$-1=0,
解得:$\frac{m}{n}$=$\frac{-1±\sqrt{5}}{2}$(负值舍去),
∴$\frac{m}{n}$=$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查了平行线的性质、等腰三角形的性质、三角形内角和定理、全等三角形的判定与性质、折叠的性质、相似三角形的判定与性质、解一元二次方程等知识;熟练掌握相似三角形的判定与性质是解决问题的关键.

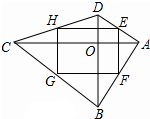 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )| A. | AC平分BD | B. | AC⊥BD | C. | AC=BD | D. | AC与BD互相平分 |
| A. | x-3 | B. | 3-x | C. | x+3 | D. | ±(x-3) |
 已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.
已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.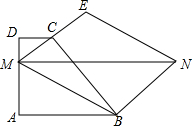 如图,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M是线段AD上任意一点,连接MC并延长到点E,使MC=CE,以MB和ME为边作平行四边形MBNE,请直接写出线段MN长度的最小值.
如图,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M是线段AD上任意一点,连接MC并延长到点E,使MC=CE,以MB和ME为边作平行四边形MBNE,请直接写出线段MN长度的最小值.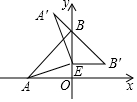 如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.
如图,在平面直角坐标系中,点A(-3,0)、点B(0,3),点E在OB上,将△ABE绕点E顺时针旋转90°得到△A′B′E,则A′B′的值为3$\sqrt{2}$.