题目内容
8. 如图梯形ABCD中,AD∥BC,F为AD的中点,连接BF并延长与CD的延长线交于点E,且∠ABE=∠ACE.
如图梯形ABCD中,AD∥BC,F为AD的中点,连接BF并延长与CD的延长线交于点E,且∠ABE=∠ACE.(1)写出图中三对相似三角形(不需要证明).
(2)证明:$\frac{EF}{BE}$=$\frac{FG}{BG}$.
(3)若BG=2,EF=1,求FG的长.
分析 (1)根据相似三角形的判定方法可知:△AFG∽△CBG,△EFD∽△EBC,△AGB∽△EGC,
(2)由△EFD∽△EBC,得$\frac{EF}{EB}$=$\frac{DF}{CB}$,由△AFG∽△CBG,得$\frac{AF}{BC}$=$\frac{FG}{GB}$,因为AF=DF,由此即可证明.
(3)利用(2)的结论,设FG=x,列出方程即可解决.
解答 (1)解:∵AF∥BC,
∴△AFG∽△CBG,
∵DF∥BC,
∴△EFD∽△EBC,
∵∠ABG=∠GCE,∠AGB=∠EGC,
∴△AGB∽△EGC,
∴△AFG∽△CBG,△EFD∽△EBC,△AGB∽△EGC,
(2)证明:由(1)可知:△EFD∽△EBC,
∴$\frac{EF}{EB}$=$\frac{DF}{CB}$,
∵△AFG∽△CBG,
∴$\frac{AF}{BC}$=$\frac{FG}{GB}$,
∵AF=DF,
∴$\frac{EF}{BE}$=$\frac{FG}{GB}$.
(3)解:设FG=x,∵$\frac{EF}{BE}$=$\frac{FG}{GB}$,EF=1,BG=2,
∴$\frac{1}{3+x}$=$\frac{x}{2}$,
∴x2+3x-2=0,
∴x=$\frac{\sqrt{17}-3}{2}$或$\frac{-\sqrt{17}-3}{2}$(舍弃),
∴FG=$\frac{\sqrt{17}-3}{2}$.
点评 本题考查相似三角形的判定和性质、平行线的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,学会转化的思想,把问题转化为方程去思考,属于中考常考题型.

练习册系列答案
相关题目
20. 如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
 如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )| A. | 敬 | B. | 业 | C. | 诚 | D. | 信 |
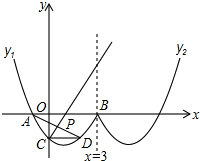 如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=$\frac{\sqrt{3}}{3}$(x2-2x-3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.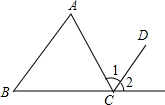 已知:如图,AB∥CD,若∠A=66°∠B=45°,则∠1=66°,∠2=45°.
已知:如图,AB∥CD,若∠A=66°∠B=45°,则∠1=66°,∠2=45°.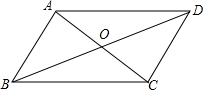 如图,?ABCD的对角线AC,BD相交于点O,△ABO的周长为23cm,AD比CD长2cm,AC与BD的和为34cm,求?ABCD的周长.
如图,?ABCD的对角线AC,BD相交于点O,△ABO的周长为23cm,AD比CD长2cm,AC与BD的和为34cm,求?ABCD的周长. 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.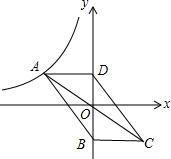 如图,点A在函数y=-$\frac{1}{x}$(x<0)的图象上,将线段AO绕点O按顺时针方向旋转180°后,得到线段CO,若点B、D在y轴上,且AD∥BC∥x轴,则四边形ABCD的面积等于2.
如图,点A在函数y=-$\frac{1}{x}$(x<0)的图象上,将线段AO绕点O按顺时针方向旋转180°后,得到线段CO,若点B、D在y轴上,且AD∥BC∥x轴,则四边形ABCD的面积等于2.