题目内容
如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）探究下列问题：
①若一个函数的特征数为[2，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[4，2]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[2，4]？
（1）此函数图象的顶点坐标为：（1，0）；（2）图象对应的函数的特征数为：[0，﹣1]；（3）原函数的图象向右平移1个单位，再向上平移5个单位得到．
【解析】试题分析：（1）根据特征数的定义，得二次函数为y=x2﹣2x+1，再利用配方得：y=（x﹣1）2，从而顶点坐标为（1,0）
（2）①根据特征数的定义，得二次函数为y=x2+2x-1，再利用配方得y=（x+1）2﹣2，图象先向右平移...
身高相同的三个小朋友甲、乙、丙放风筝，他们放出的线长分别为300m，250 m，200m；线与地面所成的角度分别为30°，45°，60°(假设风筝线是拉直的)，则三人所放的风筝（ ）
A．甲的最高 B．乙的最低 C．丙的最低 D．乙的最高
D．
【解析】
试题解析：甲放的高度为：300×sin30°=150米．
乙放的高度为：250×sin45°=125≈176.75米．
丙放的高度为：200×sin60°=100≈173.2米．
所以乙的最高．
故选D． 观察下列各组整式，其中没有公因式的是( )
A. 2a+b和a+b B. 5m(a-b) 和-a+b
C. 3(a+b) 和-a-b D. 2x+2y和2
A
【解析】选项A，没有公因式；选项B，有公因式a-b；选项C，有公因式a+b；选项D，有公因式2.故选A. 4x2-9=(2x+3)(2x-3)从左到右的变形是__________________.
因式分解
【解析】因式分解是把一个多项式化为几个整式积的形式，由此可得该变形属于因式分解. 下列各式从左到右的变形（1）15x2y=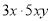
；（2）(x+y)(x-y)=x2-y2；
（3）x2-6x+9=(x-3)2；（4）x2+4x+1=x(x+4+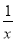
)，其中是因式分解的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得只有（3）符合要求，故选A. 已知抛物线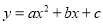
（a＜0）过A（-2，0）、O（0，0）、B（-3， 
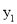）、C（3， 
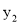）四点，则
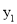与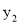
的大小关系是__________
【解析】由已知得抛物线与x轴交于A（-2，0）、O（0，0）两点，开口向下，对称轴为x==-1，可知B（-3， ）、C（3， ）两点在对称轴的两边，点B离对称轴较近，再根据抛物线图象可得．
故答案为： ． 二次函数y＝x ²－x＋m(m为常数)的图象如图所示，当x＝a时，y＜0；那么当x＝a－1时，函数值（ ）
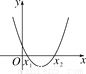
A. y＜0 B. 0＜y＜m C. y＞m D. y＝m
C
【解析】试题分析：根据对称轴及函数值判断a的取值范围，从而得出a﹣1＜0，因为当x是y随x的增大而减小，所以当x=a﹣1＜0时，函数值y一定大于m．
【解析】
当x=a时，y＜0，
则a的范围是x1＜a＜x2，
又对称轴是x=，
所以a﹣1＜0，
当x是y随x的增大而减小，
当x=0是函数值是m．
因而当x=a﹣1＜0时，函数值y一定大于m．
... 设抛物线y=ax2+bx+c(a≠0)过点A(0，2)，B(4，3)，C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为______.
y=x2-x+2或y=-x2+x+2.
【解析】试题分析：∵抛物线过A(0，2)，∴.
∵抛物线过B(4，3)，∴.
∵抛物线过C，且点C在直线上，点C到抛物线对称轴的距离等于1，
∴.
∴或，解得或.
∴抛物线的函数解析式为或. 若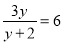
，则
=_______.
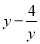-3
【解析】解方程，得：y=-4，经检验y=-4是方程的解，
所以=-4+1=-3，
故答案为：-3.