题目内容
16．设α，β为x2-x-1=0的两根，则$\frac{1}{α}$+$\frac{1}{β}$=（ ）| A． | -1 | B． | 1 | C． | 0 | D． | 2 |
分析 先根据根与系数的关系得到α+β=1，αβ=-1，再通分得到$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$，然后利用整体代入的方法计算．
解答 解：根据题意得α+β=1，αβ=-1，
所以则$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$=$\frac{1}{-1}$=-1，
故选A．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
阅读快车系列答案
相关题目
10．下列命题中真命题是（ ）
| A． | 三角形按边可分为不等边三角形，等腰三角形和等边三角形 | |
| B． | 等腰三角形任一个内角都有可能是钝角或直角 | |
| C． | 三角形的一个外角大于任何一个内角 | |
| D． | 三角形三条内角平分线相交于一点，这点到三角形三边的距离相等 |
4．已知两个质地均匀的正方体A，B，每个面上分别标有数字1，2，3，4，5，6，同时抛掷A，B，设两立方体朝上的数字分别为x，y，并以此确定点P（x，y），那么点P落在抛物线y=-x2+3x上的概率为（ ）
| A． | $\frac{1}{18}$ | B． | $\frac{1}{12}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{6}$ |
如图，抛物线y1=-x2+4x和直线y2=2x在同一直角坐标系中．当y1＞y2时，x的取值范围是0＜x＜2．
5．
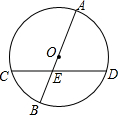如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）
如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）| A． | 2$\sqrt{21}$cm | B． | 4$\sqrt{6}$cm | C． | 2$\sqrt{22}$cm | D． | 8cm |