题目内容
11.在函数y=$\frac{\sqrt{x-2}}{x+1}$中,自变量x的取值范围是x≥2.分析 根据二次根式有意义的条件是:被开方数是非负数,以及分母不等于0,据此即可求解.
解答 解:根据题意得:$\left\{\begin{array}{l}{x-2≥0}\\{x+1≠0}\end{array}\right.$,
解得x≥2.
故答案是:x≥2.
点评 本题考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在下列命题中,是真命题的为( )
| A. | 对角线垂直的四边形是菱形 | |
| B. | 对角线垂直且相等的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
16.设α,β为x2-x-1=0的两根,则$\frac{1}{α}$+$\frac{1}{β}$=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
3.使式子$\sqrt{\frac{1}{x+1}}$有意义的x取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
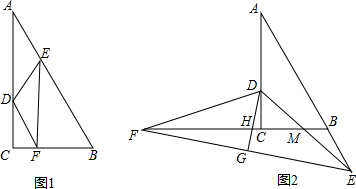
 如图,∠1=∠2,∠3+∠4=180°,问a与c的关系如何?为什么?
如图,∠1=∠2,∠3+∠4=180°,问a与c的关系如何?为什么?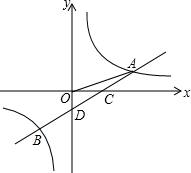 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,AE垂直x轴于E点,已知$OA=\sqrt{10}$,OE=3AE,点B的坐标为(m,-2).