题目内容
4.如图1,?ABCD 中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.(1)求证:四边形EBFD是平行四边形;
(2)小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图2)中补全他的证明思路.
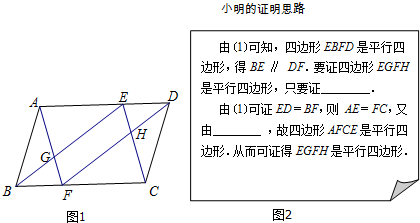
分析 (1)由平行四边形的性质得出AD∥BC,∠ABC=∠ADC.AD=BC,由角平分线得出∠ABE=∠EBC=∠ADF=∠CDF.证出EB∥DF,即可得出结论;
(2)由平行四边形的性质得出BE∥DF,DE=BF,得出AE=CF,证出四边形AFCE是平行四边形,得出GF∥EH,即可证出四边形EGFH是平行四边形.
解答 (1)证明:在?ABCD中,AD∥BC,∠ABC=∠ADC.AD=BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=$\frac{1}{2}$∠ABC.
∵DF平分∠ADC,
∴∠ADF=∠CDF=$\frac{1}{2}$∠ADC.
∵∠ABC=∠ADC.
∴∠ABE=∠EBC=∠ADF=∠CDF.
∵AD∥BC,
∴∠AEB=∠EBC.
∴∠AEB=∠ADF.
∴EB∥DF.
∵ED∥BF,
∴四边形EBFD是平行四边形.
(2)解:补全思路:GF∥EH,AE∥CF;理由如下:
∵四边形EBFD是平行四边形;
∴BE∥DF,DE=BF,
∴AE=CF,
又∵AE∥CF,
∴四边形AFCE是平行四边形,
∴GF∥EH,
∴四边形EGFH是平行四边形.
点评 此题主要考查了平行四边形的性质与判定;熟练掌握平行四边形的性质,证明EB∥DF和四边形AFCE是平行四边形,是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
14.将点A(-4,-2)向右平移5的单位长度得到点B,则点B的所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在平行四边形ABCD中,∠A:∠B:∠C=2:1:2,则∠D=( )
| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
 如图,E、F、G、H分别是?ABCD各边的中点.
如图,E、F、G、H分别是?ABCD各边的中点.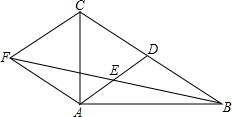 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
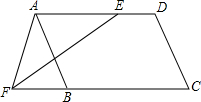 已知:如图,∠A=∠C,∠AEF=∠F.求证:AB∥CD.
已知:如图,∠A=∠C,∠AEF=∠F.求证:AB∥CD.