题目内容
13.在平面直角坐标系中,已知点A(2,0),点B(2,1),在x轴上找一点C(原点O除外),使得△ABC与△OAB相似,这样的点共有3个.分析 由点A(2,0),点B(2,1),得到OA=2,AB=1,∠OAB=90°,根据△ABC与△OAB相似,得到$\frac{AC}{AO}=\frac{AB}{AB}$=1,$\frac{AC}{AB}=\frac{AB}{AO}$=$\frac{1}{2}$,求得AC,即可得到OC,于是结论可得.
解答  解:∵点A(2,0),点B(2,1),
解:∵点A(2,0),点B(2,1),
∴OA=2,AB=1,∠OAB=90°,
∵△ABC与△OAB相似,
∴$\frac{AC}{AO}=\frac{AB}{AB}$=1,
∴AC=AO=2,
∴OC=4,
∴C(4,0),
∴$\frac{AC}{AB}=\frac{AB}{AO}$=$\frac{1}{2}$,
∴AC=$\frac{1}{2}$,
∴OC=$\frac{3}{2}$,或OC=$\frac{5}{2}$,
∴C($\frac{3}{2}$,0),($\frac{5}{2}$,0),
∴这样的点C共有3个.
故答案为:3.
点评 本题考查了坐标与图形的性质,相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
1.如果a>b,那么下列不等式中,错误的是( )
| A. | a-2>b-2 | B. | -2a>-2b | C. | $\frac{a}{2}>\frac{b}{2}$ | D. | -3a<-3b |
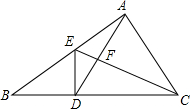 如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.
如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.