题目内容
18.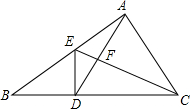 如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.
如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.
分析 根据AD=AC,得到∠ADC=∠ACD,根据线段垂直平分线的性质得到BE=CE,于是得到∠B=∠FCD,推出△ABC∽△FCD,即可得到结论.
解答 解:∵AD=AC,
∴∠ADC=∠ACD,
∵D是BC的中点,DE⊥BC,
∴BE=CE,
∴∠B=∠FCD,
∴△ABC∽△FCD,
∴$\frac{AB}{AC}=\frac{CF}{DF}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,线段垂直平分线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
9.国务院总理李克强十二届全国人大三次会议上作政府报告时说,2014年国内生产总值达到63600000000000元,这一数字用科学记数表示为( )
| A. | 636×1010 | B. | 63.6×1013 | C. | 6.36×1014 | D. | 6.36×1013 |
6.无论k取何值时,关于x,y的方程(k-1)x+(k+1)y-k+3=0均有解$\left\{\begin{array}{l}{x=m}\\{y=n}\end{array}\right.$,则m2015+n2015的值为( )
| A. | 0 | B. | -2 | C. | 22015-1 | D. | 22015-1 |
10. 如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
 如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
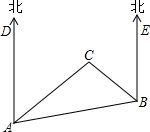 如图所示,C岛在A岛的北偏东35°方向上,B岛在A岛北偏东75°方向上,C岛在B岛的北偏西30°方向上,从C岛看A、B两岛的视角∠ACB是多少度?
如图所示,C岛在A岛的北偏东35°方向上,B岛在A岛北偏东75°方向上,C岛在B岛的北偏西30°方向上,从C岛看A、B两岛的视角∠ACB是多少度?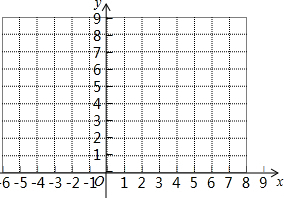 已知二次函数y=a(x-h)2+k(a≠0)的图象经过原点,当x=-2时,函数有最小值为-2.
已知二次函数y=a(x-h)2+k(a≠0)的图象经过原点,当x=-2时,函数有最小值为-2.