题目内容
5.端午节包粽子是我国的习俗,有些粽子像一个四面体(如图1),某同学想用一个内角为60°的平行四边形纸条折成一个正四面体(每个面是正三角形,如图2),然后做成一种端午节饰品(如图3),已知正四面体的棱长为4cm,每个面需要5层纸叠合,那么所用的平行四边形纸条的较长的边长(纸片的厚度忽略不计)至少是( )
| A. | 30cm | B. | 40cm | C. | 50cm | D. | 60cm |
分析 根据正四面体的展开图中的边长,求得所用的平行四边形纸条的较长的边长.
解答 解:如图所示,将正四面体沿着一些棱剪开,展平可得平行四边形的展开图:
∵正四面体的棱长为4cm,每个面需要5层纸叠合,
∴所用的平行四边形纸条的较长的边长至少为:8×5=40cm,
故选:B.
点评 本题主要考查了折叠问题,等边三角形的性质,解题时需要掌握正四面体的展开图的特征.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.

练习册系列答案
相关题目
17.已知关于x的方程x2+2x+k=0没有实数根,则k的取值范围是( )
| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
15.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
10.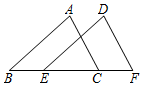 如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )
 如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )
如图,在△ABC和△DEF中,已知∠B=∠DEF,AB=ED,加上该条件后仍无法证明△ABC≌△DEF的是( )| A. | AC=DF | B. | BE=CF | C. | AC∥DF | D. | ∠A=∠D |
14.下列不等式中,是一元一次不等式的是( )
| A. | x+1>2 | B. | x2>9 | C. | 2x+y≤5 | D. | $\frac{1}{x}$>3 |
15.已知x=1是方程x2+mx+n=0的一个根,则代数式m2+2mn+n2的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
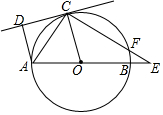 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.
如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.