题目内容
4.已知反比例函数$y=\frac{k}{x}$和一次函数y=mx的图象都经过第一象限的点A,点B在x轴正半轴上,O是坐标原点,△ABO是直角边长为2的等腰直角三角形.(1)实数k和m的值;
(2)设点C(-m,k),求经过点C的反比例函数图象的解析式,并说出满足条件的反比例函数图象的共同特征(至少2个).

分析 (1)根据题意可以分两种情况,然后画出相应的图形,从而可以得到k和m的值;
(2)由(1)可知两种情况下的点C的坐标,从而可以分别求出相应的反比例函数的解析式,进而可以写出满足条件的反比例函数图象的共同特征.
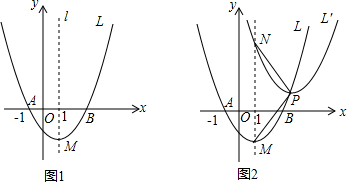
解答  解:(1)当∠ABO=90°且OB=AB时,如右图(1)所示,
解:(1)当∠ABO=90°且OB=AB时,如右图(1)所示,
∵OB=AB=2,
∴点A(2,2),
∵反比例函数$y=\frac{k}{x}$和一次函数y=mx的图象都经过第一象限的点A,
∴$2=\frac{k}{2}$,2=2m,
解得,k=4,m=1;
当∠OAB=90°且OA=AB=2时,如图(2)所示,
则∠AOB=45°,
∴点A($\sqrt{2},\sqrt{2}$)
∵反比例函数$y=\frac{k}{x}$和一次函数y=mx的图象都经过第一象限的点A,
∴$\sqrt{2}=\frac{k}{\sqrt{2}}$,$\sqrt{2}=\sqrt{2}m$,
解得,k=2,m=1;
(2)设反比例函数$y=\frac{n}{x}$,
当k=4,m=1时,则点C为(-1,4),
∵反比例函数$y=\frac{n}{x}$的图象过点C(-1,4),
∴$4=\frac{n}{-1}$,
解得,n=-4,
∴过点C的反比例函数图象的解析式为$y=\frac{-4}{x}$;
当k=2,m=1时,则点C为(-1,2),
∵反比例函数$y=\frac{n}{x}$的图象过点C(-1,2),
∴$2=\frac{n}{-1}$,
解得,n=-2,
∴过点C的反比例函数图象的解析式为$y=\frac{-2}{x}$;
满足条件的反比例函数图象的共同特征:①图象都在二、四象限;②在每个象限,y随x的增大而增大;③函数图象关于原点对称.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和分类讨论的数学思想解答.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
| A. | m2<n2 | B. | m-n>0 | C. | m-3<n-3 | D. | -m<-n |
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
| 监测点 | 荔园 | 西乡 | 华侨城 | 南油 | 盐田 | 龙岗 | 洪湖 | 南澳 | 葵涌 | 梅沙 | 观澜 |
| AQI | 15 | 31 | 25 | 24 | 31 | 24 | 25 | 25 | 34 | 20 | 26 |
| 质量 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 | 优 |
| A. | 25,25 | B. | 31,25 | C. | 25,24 | D. | 31,24 |
| A. | 2x+x=2x2 | B. | 2x2-x2=2 | C. | 2x2•3x2=6x4 | D. | 2x6÷x2=2x3 |