题目内容
19．方程（x-2）2=b的解的情况是（ ）| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 没有实数根 | D． | 无法确定 |
分析 分三种情况：①b＞0；②b=0；③b＜0；进行讨论可求方程（x-2）2=b的解的情况．
解答 解：①b＞0，方程（x-2）2=b有两个不相等的实数根；
②b=0，方程（x-2）2=b有两个相等的实数根；
③b＜0，方程（x-2）2=b没有实数根．
故选：D．
点评 考查了根的判别式，本题直接根据完全平方数是非负数求解，注意分类思想的应用．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
9．
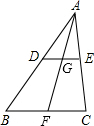如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，F为BC边上一点，连接AF交DE于点G，下列说法不正确的是（ ）
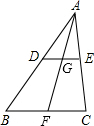如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，F为BC边上一点，连接AF交DE于点G，下列说法不正确的是（ ）| A． | $\frac{DG}{GE}$=$\frac{BF}{FC}$ | B． | $\frac{DG}{BF}$=$\frac{DE}{BC}$ | C． | $\frac{AD}{DB}$=$\frac{BF}{FC}$ | D． | $\frac{AD}{AE}$=$\frac{AB}{AC}$ |
10．下列计算正确的是（ ）
| A． | （a2）3=a5 | B． | （ab2）2=ab4 | C． | a4÷a=a4 | D． | a2•a2=a4 |
11．在-3、0、1、-2四个数中，最小的数为（ ）
| A． | -3 | B． | 0 | C． | 1 | D． | -2 |
8．某工厂计划每天生产x吨生产资料，采用新技术后每天多生产3吨，实际生产180吨与原计划生产120吨的时间相等，那么适合x的方程是（ ）
| A． | $\frac{120}{x+3}=\frac{180}{x}$ | B． | $\frac{120}{x-3}=\frac{180}{x}$ | C． | $\frac{120}{x}=\frac{180}{x+3}$ | D． | $\frac{120}{x}=\frac{180}{x-3}$ |
9．八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（ ）
| A． | $\frac{10}{x}$-$\frac{10}{2x}$=20 | B． | $\frac{10}{2x}$-$\frac{10}{x}$=20 | C． | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{3}$ | D． | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{3}$ |