题目内容
14. 如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=2.
如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=2.
分析 作PE⊥OA于E,根据角平分线的性质可得PE=PD,根据平行线的性质可得∠ACP=∠AOB=30°,由直角三角形中30°的角所对的直角边等于斜边的一半,可求得PE,即可求得PD.
解答  解:作PE⊥OA于E,
解:作PE⊥OA于E,
∵∠AOP=∠BOP,PD⊥OB,PE⊥OA,
∴PE=PD(角平分线上的点到角两边的距离相等),
∵∠BOP=∠AOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴在Rt△PCE中,PE=$\frac{1}{2}$PC=$\frac{1}{2}$×4=2(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴PD=PE=2,
故答案是:2.
点评 此题主要考查角平分线的性质和平行线的性质,难度一般,作辅助线是关键.

练习册系列答案
相关题目
2.下列关于x的方程中,一定有实数根的是( )
| A. | $\sqrt{x}$+1=0 | B. | $\sqrt{x}$=-x | C. | $\sqrt{{x}^{2}+3}$=0 | D. | $\frac{x}{x-1}$=$\frac{1}{x-1}$ |
19.不等式$\frac{x}{2}$-$\frac{x-1}{3}$≤1的解集是( )
| A. | x≤4 | B. | x≥4 | C. | x≤-1 | D. | x≥-1 |
 如图,正方形ABCD和正方形AEFG中,点E在AD上,如果AB=3,那么△BDF的面积等于4.5.
如图,正方形ABCD和正方形AEFG中,点E在AD上,如果AB=3,那么△BDF的面积等于4.5.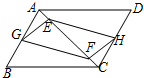 如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,E,F是对角线AC上的两个动点,分别从A,C处同时出发相向而行,到C,A时停止运动.若两动点的速度均为1cm/s,AB=14cm,BC=18cm,AC=24cm,经t秒后,四边形GFHE为矩形,则此时t的值为3或21.
如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,E,F是对角线AC上的两个动点,分别从A,C处同时出发相向而行,到C,A时停止运动.若两动点的速度均为1cm/s,AB=14cm,BC=18cm,AC=24cm,经t秒后,四边形GFHE为矩形,则此时t的值为3或21.