Question

13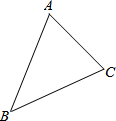．画图并讨论：已知△ABC，如图所示，要求画一个三角形，使它与△ABC有一个公共的顶点C，并且与△ABC全等．
（1）甲同学的画法是：
①延长BC和AC；
②在BC的延长线上取点D，使CD=BC；
③在AC的延长线上取点E，使CE=AC；
④连结DE，得△DEC．
（2）乙同学的画法是：
①延长AC和BC；
②在BC的延长线上取点M，使CM=AC；
③在AC的延长线上取点N，使CN=BC；
④连结MN，得△MNC．
究竟哪种画法对，有如下几种可能：
①甲画得对，乙画得不对；②甲画的不对，乙画得对；③甲、乙都画得对；④甲、乙都画得不对；正确的结论是③．（请填序号）
（3）这道题还可这样完成：
①用量角器量出∠ACB的度数；
②在∠ACB的外部画射线CP，使∠ACP=∠ACB；
③在射线CP上取点D，使CD=CB；
④连结AD，△ADC就是所要画的三角形．
这样画的结果可记作△ABC≌△ADC．
（4）满足题目要求的三角形可以画出多少个呢？答案是无数个．
（5）请你再设计一种画法，在图中画出图形，简要说明画法不必说明理由．

Answer 1

分析 （1）、（2）利用“SAS”可甲乙的画法进行判断；
（3）根据“SAS”可判断△ABC≌△ADC；
（4）以BC为公共边画三角形与△ABC全等．

解答 解：（1）、（2）对于甲的画法，可根据“SAS”判定△ACB≌△ECD；对于乙的画法，可根据“SAS”判定△ACB≌△MCN，所以甲、乙都画得对；
（3）根据“SAS”可判断△ABC≌△ADC；
（4）满足题目要求的三角形可以画出无数个；
（5）如图，过C点作CE∥AB，截取CE=AB，连结BE，则△BCE为所作．

故答案为③，△ADC，无数．

点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．