题目内容
15.计算:$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{{x}^{2}-x}{x-1}$÷x.分析 首先将分子与分母因式分解进而化简得出即可.
解答 解:$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$+$\frac{{x}^{2}-x}{x-1}$÷x
=$\frac{(x-2)(x+2)}{(x-2)^{2}}$+1
=$\frac{x+2}{x-2}$+$\frac{x-2}{x-2}$
=$\frac{2x}{x-2}$.
点评 此题主要考查了分式的化简求值,正确因式分解得出是解题关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
5.对于二次函数y=-2(x+4)2-3和它的图象,下列说法错误的是( )
| A. | 抛物线开口向下 | B. | y随x的增大而减小 | ||
| C. | 抛物线关于直线x=-4对称 | D. | 抛物线不会经过第一象限 |
20.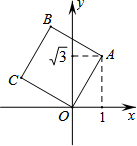 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点C的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-$\sqrt{3}$,1) | C. | (-2,1) | D. | (-1,2) |
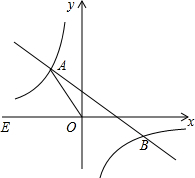 在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.
在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.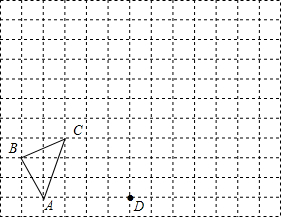 如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;