题目内容
6.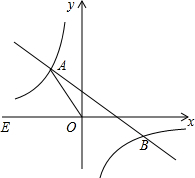 在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.
在平面直角坐标系xOy中,一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于二、四象限内的A、B两点,若点A纵、横坐标绝对值的比为4:3.(1)求反比例函数解析式;
(2)求△AOB的面积.
分析 (1)先设A点坐标是(a,b),根据点A纵、横坐标绝对值的比为4:3,易知$\frac{b}{a}=-\frac{4}{3}$①,再把(a,b)代入一次函数解析式可得$b=-\frac{2}{3}a+2$②,两式联合可求a、b,再把a、b的值代入反比例函数,即可求k,从而可得反比例函数解析式;
(2)先求出一次函数与x轴的交点D的坐标,再求出一次函数与反比例函数的另一交点B的坐标,利用S△AOB=S△AOD+S△BOD,易求△AOB的面积.
解答 (1)过A作AC⊥x轴于C,设A点坐标是(a,b),则$\frac{b}{a}=-\frac{4}{3}$①,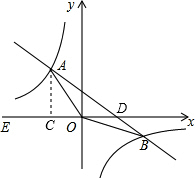
把A点坐标代入一次函数,得$b=-\frac{2}{3}a+2$②,
①②联合解得$\left\{\begin{array}{l}{a=-3}\\{b=4}\end{array}\right.$,
把A(-3,4)代入反比例函数,得k=-12,
∴反比例函数的解析式是$y=-\frac{12}{x}$;
(2)令y=0,则0=-$\frac{2}{3}$x+2,解得x=3,
∴一次函数数$y=-\frac{2}{3}x+2$与x轴的交点D的坐标是(3,0),
解$\left\{\begin{array}{l}{y=-\frac{2}{3}x+2}\\{y=-\frac{12}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-3}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=-2}\end{array}\right.$
∴一次函数与反比例函数的另一个交点B的坐标是(6,-2),
∴${S_{△AOB}}={S_{△AOD}}+{S_{△BOD}}=\frac{1}{2}×3×4+\frac{1}{2}×3×2=9$.
点评 本题考查了一次函数与反比例函数的交点问题,解题的关键是理解点和解析式的关系,以及采用分割法求三角形的面积.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案| A. | -x7y13 | B. | x3y3 | C. | x8y11 | D. | -x7y8 |
①b2-4ac>0;
②x1+x2=2h;
③二次函数y=ax2+bx+2c(a≠0)化为顶点式为y=a(x-h)2+2k;
④若c=k,则一定有h=b.
正确的有( )
| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
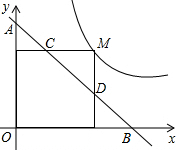 如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )
如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

| A. | 3块 | B. | 4块 | C. | 5块 | D. | 6块 |
 已知等腰直角△AOB,△CBD,双曲线y=$\frac{k}{x}$经过二个直角顶点A,C,D(6,0),求k.
已知等腰直角△AOB,△CBD,双曲线y=$\frac{k}{x}$经过二个直角顶点A,C,D(6,0),求k.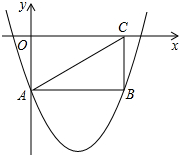 如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.