题目内容
3. 如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
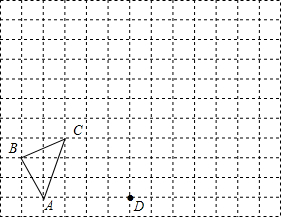
如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;(1)若点A、C的坐标分别为(-3,0)、(-2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
分析 (1)根据A,C点坐标作出直角坐标系,进而求出B点坐标;
(2)根据轴对称的性质结合平移的性质得出答案;
(3)利用位似图形的性质得出对应点位置进而得出答案.
解答  解:(1)如图所示,B(-4,2);
解:(1)如图所示,B(-4,2);
(2)如图所示:△A1B1C1即为所求;
(3)如图所示:△A2B2C2即为所求.
点评 此题主要考查了位似变换、轴对称变换和平移变换,根据题意建立正确的坐标系是解题关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
13.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{64}$=4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
11. 如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )
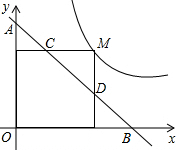
如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )
 如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )
如图,M为双曲线y=$\frac{1}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B.则AD•BC的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.由若干个相同的小立方体搭成的几何体的三视图如图所示,则组成该几何体的小立方体有( )


| A. | 3块 | B. | 4块 | C. | 5块 | D. | 6块 |
8. 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
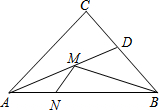
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )| A. | $3\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 6 |
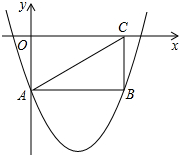 如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.