题目内容
20. 如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )| A. | $\frac{DE}{BC}$=$\frac{2}{3}$ | B. | $\frac{DE}{BC}$=$\frac{3}{5}$ | C. | $\frac{AE}{AC}$=$\frac{2}{3}$ | D. | $\frac{AE}{AC}$=$\frac{2}{5}$ |
分析 利用如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边可对各选项进行判断.
解答 解:当$\frac{AE}{AC}$=$\frac{AD}{AB}$时,DE∥BC,即$\frac{AE}{AC}$=$\frac{2}{5}$.
故选D.
点评 本题考查了平行线分线段成比例:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
10.已知⊙O的半径为$\sqrt{3}$,点P到圆心O的距离为2,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
11. 如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
 如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )
如图,△ABC≌△ADE,若∠B=80°,∠C=35°,∠EAC=40°,则∠DAC=( )| A. | 40° | B. | 35° | C. | 30° | D. | 25° |
8.已知△ABC≌△DEF,若△ABC的周长为20,AB=5,BC=6,则DF的长度为( )
| A. | 5 | B. | 6 | C. | 9 | D. | 11 |
15.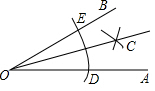 在数学课上,老师用直尺和圆规作角平分线,方法如下:
在数学课上,老师用直尺和圆规作角平分线,方法如下:
作法:①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以D、E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
说说老师用尺规作角平分线时,用到的三角形全等的判定方法是( )
 在数学课上,老师用直尺和圆规作角平分线,方法如下:
在数学课上,老师用直尺和圆规作角平分线,方法如下:作法:①在OA和OB上分别截取OD、OE,使OD=OE.
②分别以D、E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内交于点C
③作射线OC,则OC就是∠AOB的平分线
说说老师用尺规作角平分线时,用到的三角形全等的判定方法是( )
| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
12.平面直角坐标系内与点P(-2,3)关于原点对称的点的坐标是( )
| A. | (3,-2) | B. | (2,3) | C. | (2,-3) | D. | (-3,-3) |
10.下列语句中,不是命题的是( )
| A. | 锐角小于它的余角 | B. | 钝角大于它的补角 | ||
| C. | 同旁内角互补 | D. | 过点A画直线l的垂线 |
 如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.
如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.