题目内容
5.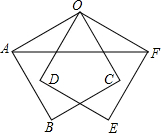 如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.
如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.
分析 先过O作OG⊥AF于G,根据∠AOF=120°,可得∠OAG=30°,进而得到Rt△AOG中,OG=$\frac{1}{2}$AO=1,再根据勾股定理求得AG的长,最后求得AF长.
解答 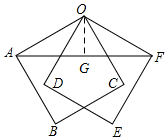 解:过O作OG⊥AF于G,则
解:过O作OG⊥AF于G,则
∵OA=OF,
∴AG=FG,
∵∠AOD=30°,
∴∠AOF=∠AOD+∠DOF=30°+90°=120°,
∴∠OAG=30°,
∴Rt△AOG中,OG=$\frac{1}{2}$AO=1,
∴AG=$\sqrt{A{O}^{2}-O{G}^{2}}$=$\sqrt{3}$,
∴AF=2AG=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题主要考查了正方形的性质,旋转的性质以及等腰三角形的性质的综合应用,解决问题的关键是作辅助线,运用等腰三角形的三线合一的性质进行计算.

练习册系列答案
相关题目
16.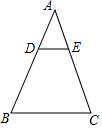 如图,在△ABC中,已知点D在AB上,DB=2AD,DE∥BC交AC于E,则下列结论正确的有( )
如图,在△ABC中,已知点D在AB上,DB=2AD,DE∥BC交AC于E,则下列结论正确的有( )
①BC=2DE;②AE=$\frac{1}{3}$AC;③△ADE∽△ABC;④$\frac{BD}{BA}$=$\frac{CE}{CA}$.
 如图,在△ABC中,已知点D在AB上,DB=2AD,DE∥BC交AC于E,则下列结论正确的有( )
如图,在△ABC中,已知点D在AB上,DB=2AD,DE∥BC交AC于E,则下列结论正确的有( )①BC=2DE;②AE=$\frac{1}{3}$AC;③△ADE∽△ABC;④$\frac{BD}{BA}$=$\frac{CE}{CA}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
 如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )| A. | $\frac{DE}{BC}$=$\frac{2}{3}$ | B. | $\frac{DE}{BC}$=$\frac{3}{5}$ | C. | $\frac{AE}{AC}$=$\frac{2}{3}$ | D. | $\frac{AE}{AC}$=$\frac{2}{5}$ |
 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④4a-2b+c>0,其中正确的个数为2.
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④4a-2b+c>0,其中正确的个数为2.