题目内容
10.已知⊙O的半径为$\sqrt{3}$,点P到圆心O的距离为2,则点P与⊙O的位置关系是( )| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
分析 根据点到圆心的距离与圆的半径之间的关系:“点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内”来求解.
解答 解:由⊙O的半径为$\sqrt{3}$,点P到圆心O的距离为2,得
d>r,
则点P与⊙O的位置关系是点P在⊙O外,
故选:A.
点评 本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=r时,点在圆上;当d>r时,点在圆外;当d<r时,点在圆内.

练习册系列答案
相关题目
20. 如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
 如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是( )| A. | $\frac{DE}{BC}$=$\frac{2}{3}$ | B. | $\frac{DE}{BC}$=$\frac{3}{5}$ | C. | $\frac{AE}{AC}$=$\frac{2}{3}$ | D. | $\frac{AE}{AC}$=$\frac{2}{5}$ |
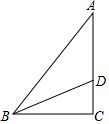 如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10.
如图:Rt△ABC中,∠C=90°,∠A=30°,BD平分∠ABC,且CD=5,则AD的长为10. 如图,已知AB∥CD,∠A=49°,∠C=27°,则∠E的度数为22°.
如图,已知AB∥CD,∠A=49°,∠C=27°,则∠E的度数为22°. 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值与最小值的差为9-$\frac{5\sqrt{2}}{2}$.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值与最小值的差为9-$\frac{5\sqrt{2}}{2}$.