题目内容
8．已知△ABC≌△DEF，若△ABC的周长为20，AB=5，BC=6，则DF的长度为（ ）| A． | 5 | B． | 6 | C． | 9 | D． | 11 |
分析 先根据三角形的周长的定义求出AC，再根据全等三角形对应角相等可得DF=AC．
解答 解：∵△ABC的周长为20，AB=5，BC=6，
∴AC=20-5-6=9，
∵△ABC≌△DEF，
∴DF=AC=9．
故选C．
点评 本题主要考查了全等三角形的性质，掌握全等三角形的对应边、对应角相等．
练习册系列答案
阅读快车系列答案
相关题目
在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，则线段EP1长度的最大值与最小值的差为9-$\frac{5\sqrt{2}}{2}$．
16．
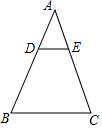如图，在△ABC中，已知点D在AB上，DB=2AD，DE∥BC交AC于E，则下列结论正确的有（ ）
①BC=2DE；②AE=$\frac{1}{3}$AC；③△ADE∽△ABC；④$\frac{BD}{BA}$=$\frac{CE}{CA}$．
如图，在△ABC中，已知点D在AB上，DB=2AD，DE∥BC交AC于E，则下列结论正确的有（ ）①BC=2DE；②AE=$\frac{1}{3}$AC；③△ADE∽△ABC；④$\frac{BD}{BA}$=$\frac{CE}{CA}$．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．在Rt△ABC中，∠C=90°，若cosB=$\frac{4}{5}$，则tanA的值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
20．
如图，在△ABC中，点D，E分别在AB，AC上，如果AD=2，BD=3，那么由下列条件能够判定DE∥BC的是（ ）
如图，在△ABC中，点D，E分别在AB，AC上，如果AD=2，BD=3，那么由下列条件能够判定DE∥BC的是（ ）| A． | $\frac{DE}{BC}$=$\frac{2}{3}$ | B． | $\frac{DE}{BC}$=$\frac{3}{5}$ | C． | $\frac{AE}{AC}$=$\frac{2}{3}$ | D． | $\frac{AE}{AC}$=$\frac{2}{5}$ |