题目内容
19.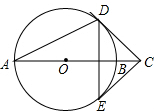 如图,AB为圆O的直径,点C是AB延长线上一点,且BC=OB,CD、CE分别与圆O相切于点D、E,若AD=5,求DE的长?
如图,AB为圆O的直径,点C是AB延长线上一点,且BC=OB,CD、CE分别与圆O相切于点D、E,若AD=5,求DE的长?
分析 连接OD,OE,AE,由于CD、CE分别与圆O相切于点D、E,得到∠ODC=∠OEC=90°,根据已知条件得到OC=2OD,求得∠DCO=30°,推出AC垂直平分DE,于是得到△ADE是等边三角形,即可得到结论.
解答 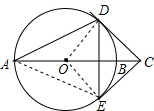 解:连接OD,OE,AE,
解:连接OD,OE,AE,
∵CD、CE分别与圆O相切于点D、E,
∴∠ODC=∠OEC=90°,
∵BC=OB,
∴OC=2OD,
∴∠DCO=30°,
∴∠DCE=60°,
∴∠DOE=120°,
∴∠DAE=60°,
∵CD=CE,∠DCO=∠ECO,
∴AC垂直平分DE,
∴AD=AE,
∴△ADE是等边三角形,
∴DE=AD=5.
点评 本题考查了切线的性质,等边三角形的判定和性质,线段垂直平分线的判定,正确的作出辅助线是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
14.下列能判定四边形是平行四边形的有( )
| A. | 一组对边相等,一组对角也相等 | |
| B. | 一组对边相等,一条对角线被另一条平分 | |
| C. | 一组对角相等,一条对角线被另一条平分 | |
| D. | 一组对角相等,过这组对角的顶点的对角线平分另一条对角线 |
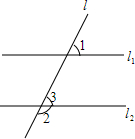 如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).
如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).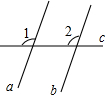 同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行)
同位角相等,两直线平行.符号语言:(如图)∵∠1=∠2(已知)∴a∥b(同位角相等,两直线平行) 如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)
如图,当具备什么条件时,AB∥EF?请说明理由(写出一个即可)