题目内容
8．
已知：如图，∠1=∠2，∠3=∠E，求证：∠A=∠CBE．
分析 由∠1=∠2，利用平行线的判定定理可得BD∥CE，由平行线的性质定理可得∠4=∠E，等量代换可得∠3=∠4，利用平行线的判定定理可得AD∥BE，易得结论．
解答 证明：∵∠1=∠2，
∴BD∥CE，
∴∠4=∠E，
∵∠3=∠E，
∴∠4=∠3，
∴AD∥BE，
∴∠A=∠CBE．
点评 本题主要考查了平行线的判定和性质定理，综合运用定理是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．下列命题的逆命题是真命题的是（ ）
| A． | 对顶角相等 | B． | 全等三角形的面积相等 | ||
| C． | 两直线平行，内错角相等 | D． | 等边三角形是等腰三角形 |
19．
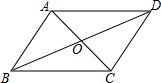如图，?ABCD的对角线相交于点O，且AB=5，△OCD的周长为23，则?ABCD的两条对角线的和是（ ）
如图，?ABCD的对角线相交于点O，且AB=5，△OCD的周长为23，则?ABCD的两条对角线的和是（ ）| A． | 18 | B． | 28 | C． | 36 | D． | 46 |
16．如果一个角的余角是60°，那么这个角的度数是（ ）
| A． | 30° | B． | 60° | C． | 90° | D． | 120° |
3．
如图，一束光线从点C出发，经过平面镜AB反射后，沿与AF平行的线段DE射出（此时∠1=∠2），若测得∠DCF=100°，则∠A=（ ）
如图，一束光线从点C出发，经过平面镜AB反射后，沿与AF平行的线段DE射出（此时∠1=∠2），若测得∠DCF=100°，则∠A=（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
13．
如图是一个正方体的表面展开图，在这个正方体中，与点A重合的点为（ ）
如图是一个正方体的表面展开图，在这个正方体中，与点A重合的点为（ ）| A． | 点C和点N | B． | 点B和点M | C． | 点C和点M | D． | 点B和点N |
20．
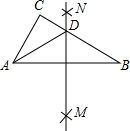如图，在△ABC中，分别以点A和点B为圆心，以大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（ ）
如图，在△ABC中，分别以点A和点B为圆心，以大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（ ）| A． | 6 | B． | 12 | C． | 16 | D． | 20 |
17．
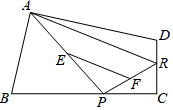如图所示，已知P、R分别是四边形ABCD的边BC、CD上的点，E、F分别是PA、PR的中点，点P在BC上从B向C移动，点R不动，那么EF的长（ ）
如图所示，已知P、R分别是四边形ABCD的边BC、CD上的点，E、F分别是PA、PR的中点，点P在BC上从B向C移动，点R不动，那么EF的长（ ）| A． | 逐渐增大 | B． | 逐渐变小 | C． | 不变 | D． | 先增大，后变小 |
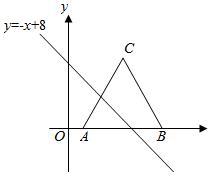如图，△ABC中，AC=BC=13，把△ABC放在平面直角坐标系xOy中，且点A，B的坐标分别为（2，0），（12，0），将△ABC沿x轴向左平移，当点C落在直线y=-x+8上时，线段AC扫过的面积为（ ）