题目内容
18.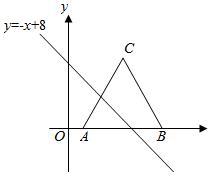 如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系xOy中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为( )
如图,△ABC中,AC=BC=13,把△ABC放在平面直角坐标系xOy中,且点A,B的坐标分别为(2,0),(12,0),将△ABC沿x轴向左平移,当点C落在直线y=-x+8上时,线段AC扫过的面积为( )| A. | 66 | B. | 108 | C. | 132 | D. | 162 |
分析 过点C作CD⊥x轴于点D,由点A、B的坐标利用勾股定理可求出点C的坐标,再利用一次函数图象上点的坐标特征可求出点C移动后的坐标,借助平行四边形的面积即可得出线段AC扫过的面积.
解答 解:过点C作CD⊥x轴于点D,如图所示.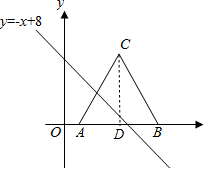
∵点A,B的坐标分别为(2,0),(12,0),AC=BC=13,
∴AD=BD=$\frac{1}{2}$AB=5,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=12.
∴点C的坐标为(7,12).
当y=12时,有12=-x+8,
解得:x=-4,
∴点C平移后的坐标为(-4,12).
∴△ABC沿x轴向左平移7-(-4)=11个单位长度,
∴线段AC扫过的面积S=11CD=132.
故选C.
点评 本题考查了一次函数图象上点的坐标特征、等腰三角形的性质、坐标与图形变化中的平移以及勾股定理,利用一次函数图象上点的坐标特征求出点C平移后的坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.为践行社会主义核心价值观,某校组织每个班进行资助贫困地区捐款活动,其中初三年级六个班捐款金额(单位:元)分别为109,109,258,272,280,355,则这组数据的中位数为( )
| A. | 109元 | B. | 265元 | C. | 272元 | D. | 280元 |
6.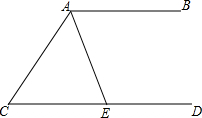 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AEC=( )
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AEC=( )
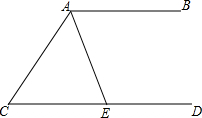 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AEC=( )
如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AEC=( )| A. | 50° | B. | 60° | C. | 65° | D. | 75° |
13.方程4x-3=x的解是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | -1 |
3.下列数中,是无理数的是( )
| A. | 0 | B. | -$\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
10.不等式2(x-1)>2的解集是( )
| A. | x<0 | B. | x>1 | C. | x>2 | D. | x>3 |
7.下列命题中,不正确的是( )
| A. | 有一组邻边相等的平行四边形是菱形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 对角线垂直的平行四边形是正方形 | |
| D. | 一组对边平行且相等的四边形是平行四边形 |
 已知:如图,∠1=∠2,∠3=∠E,求证:∠A=∠CBE.
已知:如图,∠1=∠2,∠3=∠E,求证:∠A=∠CBE.