题目内容
6. 如图,△ABC中,∠C=45°,AC=2$\sqrt{2}$,D为BC上一点,且AD=6,BD=3$\sqrt{2}$,则△ABC的周长为4$\sqrt{19}$+8$\sqrt{2}$+2.
如图,△ABC中,∠C=45°,AC=2$\sqrt{2}$,D为BC上一点,且AD=6,BD=3$\sqrt{2}$,则△ABC的周长为4$\sqrt{19}$+8$\sqrt{2}$+2.
分析 过点A作AE⊥BC,垂足为E,先求出AE和CE的长,再利用勾股定理求出DE和AB的长,进而求出△ABC的周长.
解答 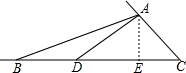 解:过点A作AE⊥BC,垂足为E,
解:过点A作AE⊥BC,垂足为E,
∵∠C=45°,AC=2$\sqrt{2}$,
∴AE=CE=2,
在△ADE中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=4$\sqrt{2}$,
∵BD=3$\sqrt{2}$,
∴BE=BD+DE=6$\sqrt{2}$,
在△AEB中,
AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=$\sqrt{72+4}$=4$\sqrt{19}$,
∴△ABC的周长为AB+BC+AC=4$\sqrt{19}$+6$\sqrt{2}$+2+2$\sqrt{2}$=4$\sqrt{19}$+8$\sqrt{2}$+2,
故答案为4$\sqrt{19}$+8$\sqrt{2}$+2
点评 本题主要考查了勾股定理的知识,解题的关键是过点A作△ABC的高,此题难度不大.

练习册系列答案
相关题目
16.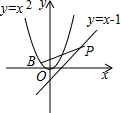 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
 如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )
如图,点P在直线y=x-1上,若存在过点P的直线交抛物线y=x2于A、B两点,且PA=AB,则称点P为“优点”,下列结论中正确的是( )| A. | 直线y=x-1上的所有点都是“优点” | |
| B. | 直线y=x-1上仅有有限个点是“优点” | |
| C. | 直线y=x-1上的所有点都不是“优点” | |
| D. | 直线y=x-1上有无穷多个点(不是所有的点)是“优点” |
 如图,边长为1的正方形ABCD的对角线交于点O,现有半径足够大的扇形OEF且∠EOF=90°,当扇形OEF绕点O转动,扇形OEF和正方形ABCD重叠部分的面积大小的规律是扇形OEF和正方形ABCD重叠部分的面积=$\frac{1}{4}$S正方形ABCD.
如图,边长为1的正方形ABCD的对角线交于点O,现有半径足够大的扇形OEF且∠EOF=90°,当扇形OEF绕点O转动,扇形OEF和正方形ABCD重叠部分的面积大小的规律是扇形OEF和正方形ABCD重叠部分的面积=$\frac{1}{4}$S正方形ABCD.